101 笔记

Surface Shading (第十章开始)

https://sites.cs.ucsb.edu/~lingqi/teaching/resources/GAMES101_Lecture_07.pdf

Z-buffer

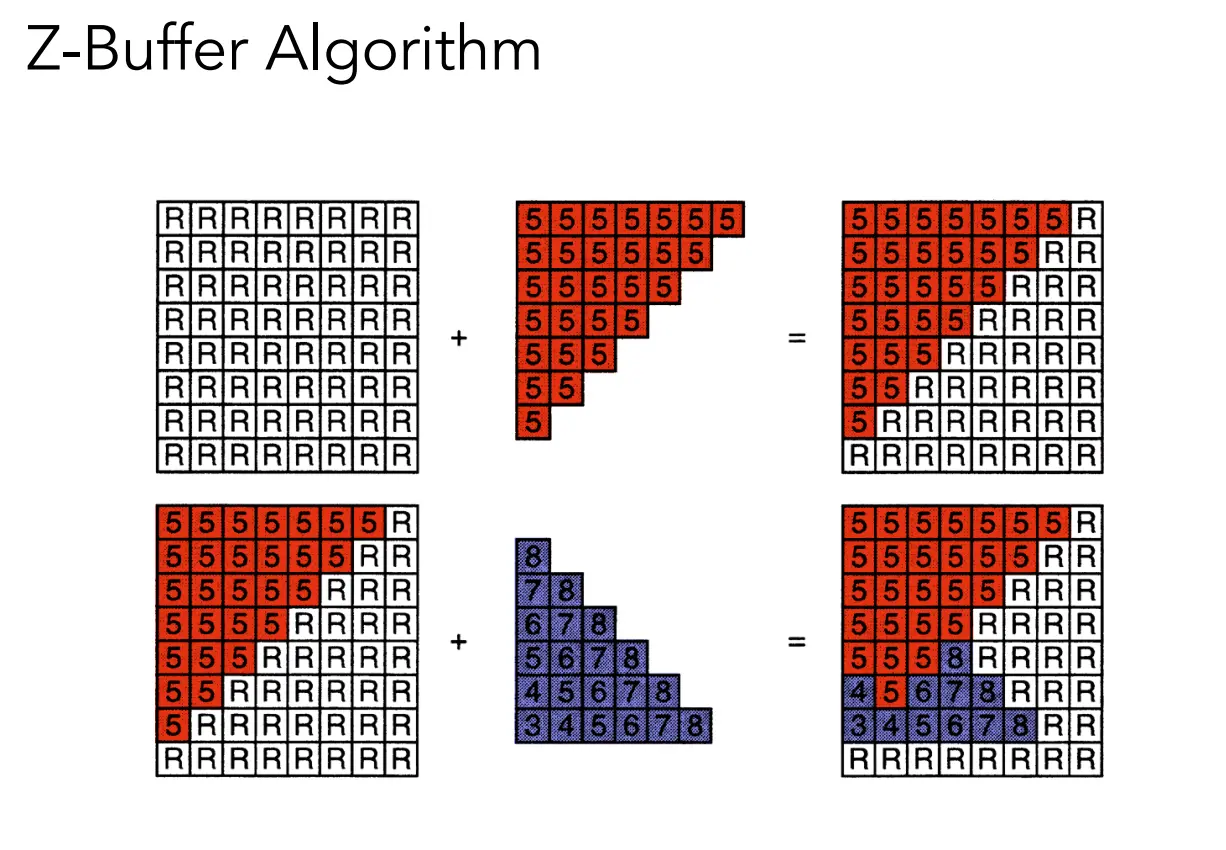
决定绘制的顺序

• Z-buffer 的思想来源于画家算法，用于处理不透明物体的遮挡问题
• Z-buffer 记录的是像素的深度，更近的会覆盖更远的，不存在排序，所以复杂度是 O(n)，本质只是记录最小（近）值
• Z-buffer 和绘制顺序无关

Shading

着色的基本构成。

• Blinn-Phong Reflectance Model = Specular highlight（镜面高光）+ Diffuse reflection（漫反射）+ Ambient light（环境光）

• Shading 是模型自身的，是local的，不考虑影子这些不属于自身的！(shading ≠ shadow)

Lambert Reflection Model

Lambert 是一种理想的漫反射光照模型 (Johann Heinrich Lambert在1760年提出)

• Lambertian Cosine Law
• Lambertian reflection 模型认为漫反射和视角方向无关
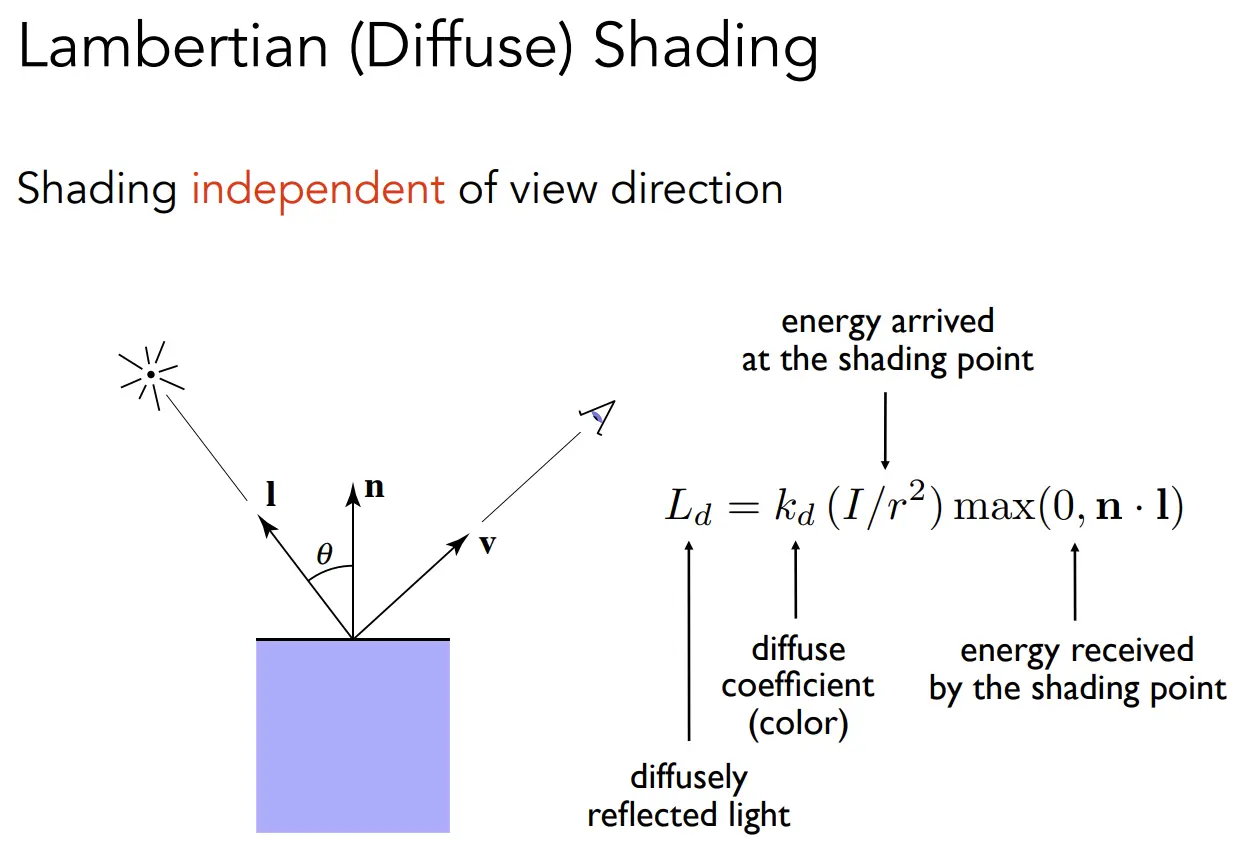
• max(0,n·l) 是为了忽略负数
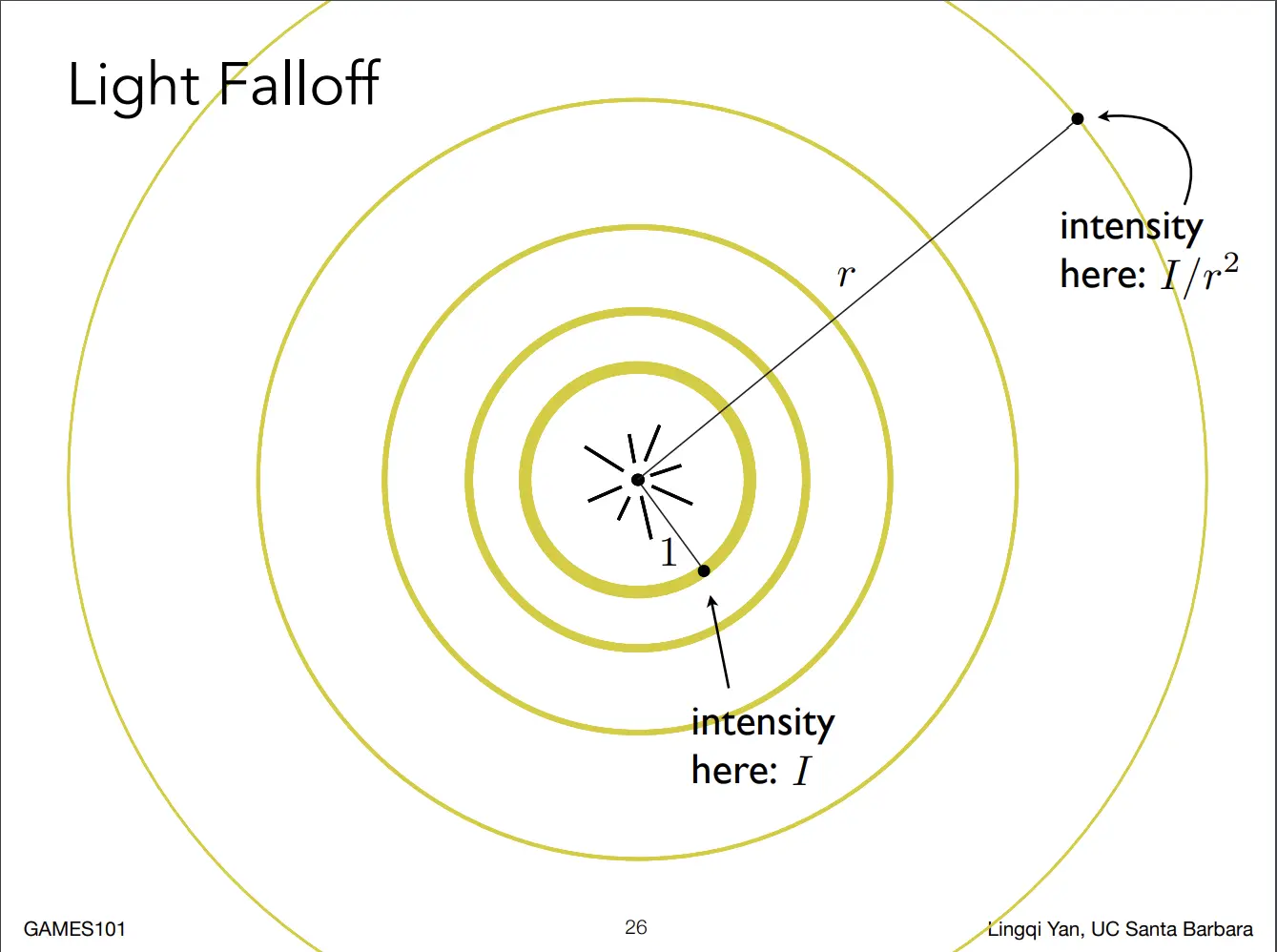
• I/r^2 能量守恒，辐射半径越远，球的表面积越大，根据面积公式可推理

补充，半Lambert

应用更广泛的是半 Lambert 模型（Half-Lambert Model）是一种用来改进标准 Lambert 光照模型的方法，广泛用于实时渲染中。

• 解决背面阴影过暗问题

  • 标准的 Lambert 模型使用点乘计算漫反射光照：

    $$I=max(0,\overrightarrow{L}\cdot \overrightarrow{N})$$

    当光源方向与法线方向点乘结果为负值时，光照强度直接为 0，这会导致模型背面完全黑暗。

  • 半 Lambert 模型通过将点乘结果调整为一个正值范围(0,1) 映射到（0.5，1) 避免背面完全黑暗的情况：

    $$I=0.5(\overrightarrow{L}\cdot \overrightarrow{N})+0.5$$

• 半 Lambert 模型适合卡通渲染、非写实渲染或游戏中需要更均匀光照的场景

• 与更复杂的光照模型相比，半 Lambert 模型计算简单，适合实时渲染的性能需求, 使用半 Lambert 模型可以在性能和效果之间取得平衡

Blinn-Phong Reflectance Model

• Blinn-Phong Reflectance Model 结合了 Lambertian 模型，集大成者（h与视角有关）

• Blinn-Phong 模型中的高光计算源于Lambertian的模型。

• 高光使用半程向量计算，是为了简化计算量，是很聪明的方式

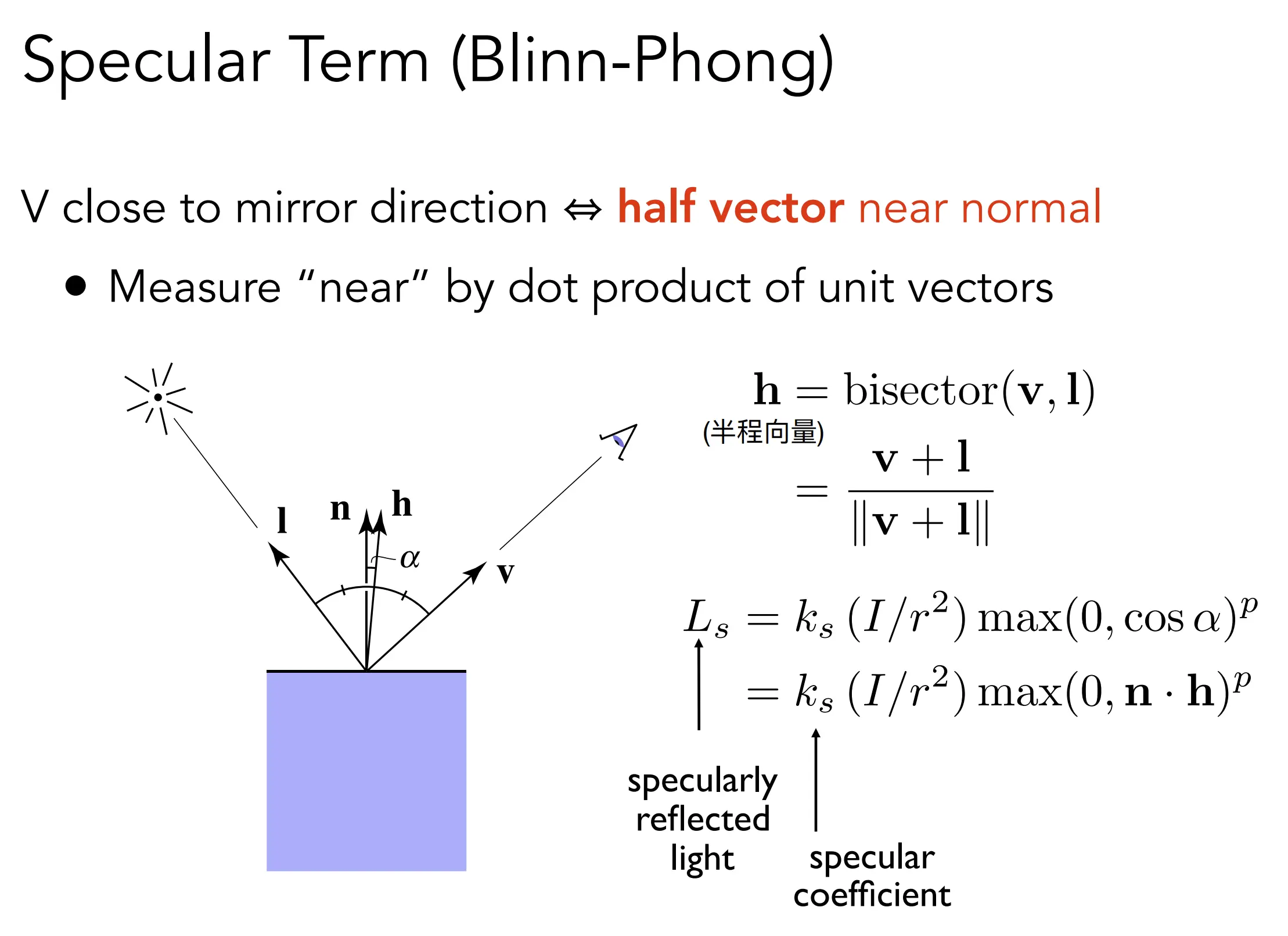
• 指数部分用于控制高光的锐利程度，通常取值范围在1-100之间，指数越高，即使较小的角度变化，过渡也越迅速

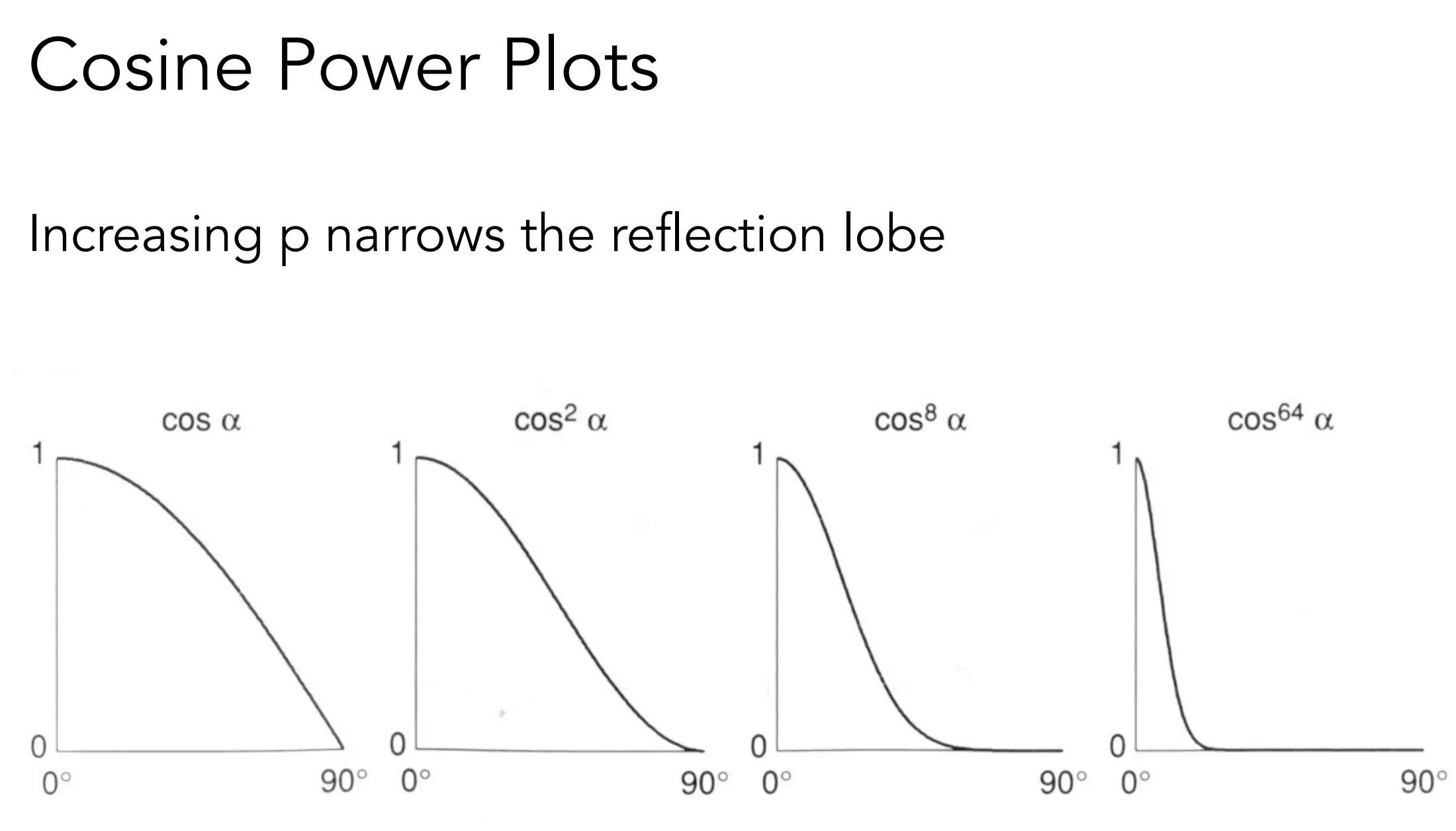
• Shading 可以发生在 Vertex Shader（顶点着色器）和 Fragment Shader（片段着色器）:

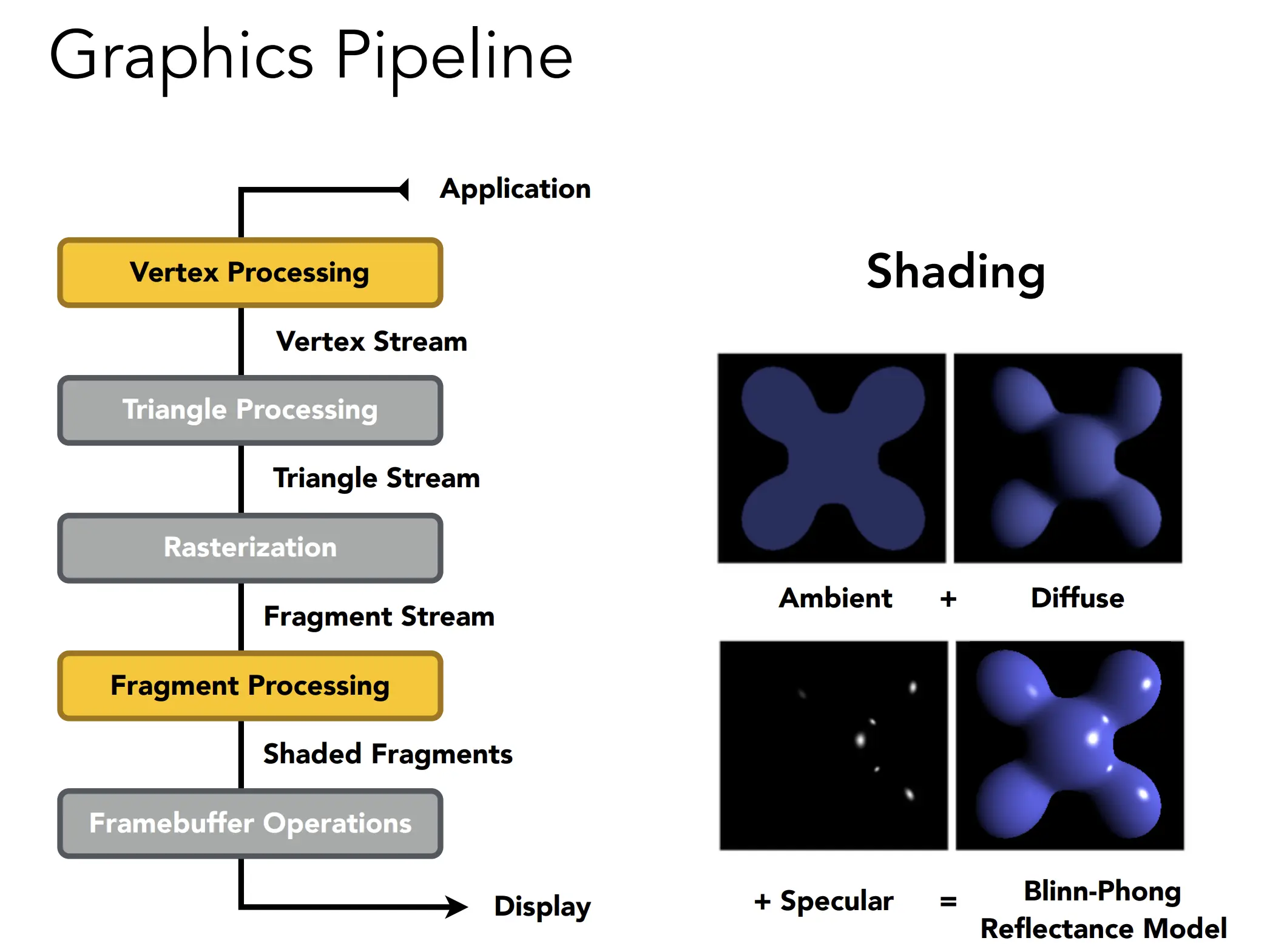
Shading Frequencies

着色频率，是指按面、顶点、像素。这里模型是纯色，所以这里的着色其实是指颜色的强度。

https://sites.cs.ucsb.edu/~lingqi/teaching/resources/GAMES101_Lecture_08.pdf

1. Flat Shading

Flat Shading（平面着色）是一种最简单的着色方法，给每个多边形（通常是三角形）分配一个统一的颜色(准确地说，是统一的光照强度乘以固有色，也就是diffuse)。

特点：

• 光照计算位置：在每个多边形的一个点（通常是顶点或质心）进行光照计算。
• 插值方式：不进行插值，整个多边形用相同的颜色。
• 效果：
  • 每个多边形表现为一个独立的平面，边界明显，具有“低多边形”风格。
  • 表面看起来不够光滑，但计算速度快，适用于性能要求高的场景（如低分辨率的实时渲染）。

优缺点：

• 优点：简单，计算量小，适合低细节的模型。
• 缺点：效果生硬，难以表现曲面细节和平滑光照。

---

2. Gouraud Shading

Gouraud Shading（高洛德着色）是一种改进的着色方法，通过插值光照值来实现更平滑的效果。

特点：

• 光照计算位置：在多边形的顶点处计算光照。
• 插值方式：将顶点计算出的光照值（颜色）线性插值到整个多边形（如果高光附近存在多个顶点，就会出现多个高光）。
• 效果：
  • 光滑过渡，避免了 Flat Shading 中的“硬边”效果。
  • 表现复杂曲面时有一定的能力，但高光区域可能会丢失细节（例如，可能高光只出现在顶点，而不会平滑扩展到中间区域）。

优缺点：

• 优点：计算量适中，效果平滑，适合大多数实时渲染。
• 缺点：无法很好表现高光等复杂光照细节。

3. Phong Shading

Phong Shading（冯氏着色）是一种更高级的着色方法，通过插值法线向量来计算像素级光照。

特点：

• 光照计算位置：在每个像素（片段）计算光照。
• 插值方式：先对顶点法线进行插值，再用插值后的法线计算每个像素的光照。
• 效果：
  • 表面表现极为光滑，可以清晰地表现高光、阴影和其他复杂光照效果。
  • 是基于像素的光照计算方法，比 Gouraud Shading 更精确。

优缺点：

• 优点：效果逼真，能精确表现高光、阴影和表面细节。
• 缺点：计算量大，尤其在像素密度高的场景中。

需要注意的是，Phong Shading 是让上色的效果更加平滑，无法解决低模型边缘锯齿问题。解决这个问题是方法是基于法向插值的平滑着色(Smooth Shading)，后续会讲。

补充，Shadow Mapping

https://sites.cs.ucsb.edu/~lingqi/teaching/resources/GAMES101_Lecture_12.pdf

光看不见的地方就是阴影。

• 前面提到的Shading, 都是对物体自身进行着色，不考虑它自己产生的其他影响，比如阴影。

• Shadow Mapping 算是一种后期处理。

• 步骤：

  • 在光源处用虚拟摄像机记录一次场景深度值，也就是Shadow Map
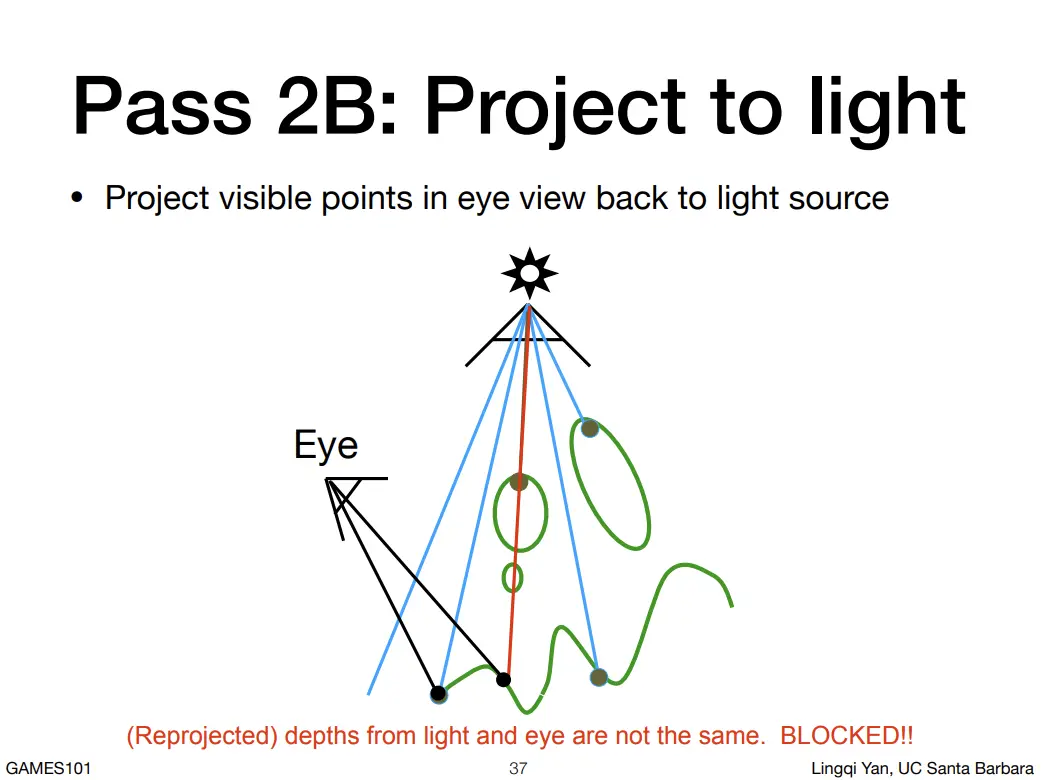
  • 在眼睛处，也就是摄像机处，查询每个可见像素，在Shadow Map上的深度值，和投射回光源处的深度值，做比较。如果几乎相同，就认为没用遮挡，可以看到光源。如果比shadow map中的深度值大，就认为有遮挡，无法看到光源，说明这个像素要被渲染成阴影。

• 也就是说，对于动态的shadow mapping, 需要做两趟光栅化操作。

  • 第一趟光栅化：从光源视角生成深度贴图 (Depth Map)
  • 第二趟光栅化：从摄像机视角渲染场景并计算阴影

• 然而，shadow map 还有非常多的问题，如图绿色的阴影并不完美。

  • 浮点数精度问题，需要添加bias, tolerance 部分解决
  • shadow map 的分辨率对结果影响很大
  • 理论上只能产生 hard shadow，无法做 soft shadow
  • soft shadow 是光源的大小决定的，比如日食在伴影区域看到的就是soft shadow,而在本影看到的就是hard shadow，全日食。

Shadow Mapping 增强方案

课程里没讲shadow mapping各种问题如何解决，我找了一些相关资料

Details

Shadow Mapping 的精度问题主要体现在阴影边缘的锯齿和深度值的精度丢失，这些问题通常是由于深度贴图分辨率有限和深度值的非线性分布造成的。以下是常见的解决方法：

---

1. 增加深度贴图分辨率

• 原理： 提高深度贴图的分辨率可以减少每个像素覆盖的世界空间范围，从而提高阴影边缘的精度。
• 缺点： 增加分辨率会显著增加内存和计算开销。

---

2. 使用级联阴影映射 (Cascaded Shadow Mapping, CSM)

• 原理： 将深度贴图划分为多个区域（级联），每个区域覆盖摄像机视锥的不同部分。
  • 近处区域使用高分辨率的深度贴图，远处区域使用低分辨率。
• 优点： 平衡了近处和远处阴影的精度。
• 缺点： 实现较复杂，需要额外的计算。

---

3. 使用深度偏移 (Depth Bias)

• 原理： 在阴影计算中，为避免由于有限精度导致的自阴影伪影（Self-Shadowing），对深度值增加一个小的偏移值。
• 缺点： 偏移值过大会导致阴影“漂浮”，过小无法完全解决自阴影问题。
• 改进： 动态偏移（基于斜率调整偏移量）。

---

4. 透视分布的深度贴图 (Perspective Shadow Mapping, PSM)

• 原理： 根据摄像机的位置，重新调整深度贴图的分布，使得更多分辨率用于靠近摄像机的区域。
• 优点： 提高了靠近摄像机区域阴影的精度。
• 缺点： 实现复杂，可能引入失真。

---

5. 使用PCF (Percentage-Closer Filtering) 滤波

• 原理： 对深度贴图的多个相邻像素进行采样，并对阴影结果进行插值。
• 优点： 平滑阴影边缘，减少锯齿。
• 缺点： 增加了采样次数和计算开销。

---

6. VSM (Variance Shadow Mapping)

• 原理： 存储深度的期望值和平方期望值，利用统计方法计算阴影概率。
• 优点： 支持软阴影，边缘过渡自然。
• 缺点： 可能出现光晕伪影（Light Bleeding）。

---

7. EVSM (Exponential Variance Shadow Mapping)

• 原理： 在 VSM 的基础上使用指数变换减少光晕伪影。
• 优点： 更精确的阴影边缘处理，适合复杂场景。
• 缺点： 需要额外的计算和内存。

---

8. 层次深度贴图 (Hierarchical Shadow Mapping)

• 原理： 使用多级深度贴图，每级分辨率逐渐递减。
• 优点： 提高整体阴影质量，同时优化性能。

---

9. 使用高精度深度缓冲 (比如 32-bit Float)

• 原理： 使用更高精度的浮点数存储深度值。
• 优点： 减少深度值精度丢失，特别是在大范围场景中。
• 缺点： 增加存储和计算开销。

---

10. 特殊投影矩阵 (LiSPSM, Logarithmic Shadow Mapping)

• 原理： 重新调整深度贴图的分布，使得更大的分辨率用于近距离和重要区域。
• 优点： 在大范围场景中有效。
• 缺点： 复杂度高，可能引入失真。

---

总结

实际应用中，通常会组合使用以上方法，例如结合PCF 滤波和级联阴影映射，以平衡精度和性能。此外，针对特定场景需求，优化深度贴图的分布是解决精度问题的关键。

插值、高级纹理映射

阅读材料：第 11 章（Texture Mapping）, 第 11.1、11.2 节

https://sites.cs.ucsb.edu/~lingqi/teaching/resources/GAMES101_Lecture_09.pdf

三角形的重心

• 重心坐标系 不依赖世界坐标，它是针对三角形三个点的相对坐标。

• 重心坐标系本质上是一种权重系统，定义了三角形顶点对任意三角形内部点的"贡献"。

• 三角形的重心，相当于这个坐标系的"0点"，三个顶点的均值位置。

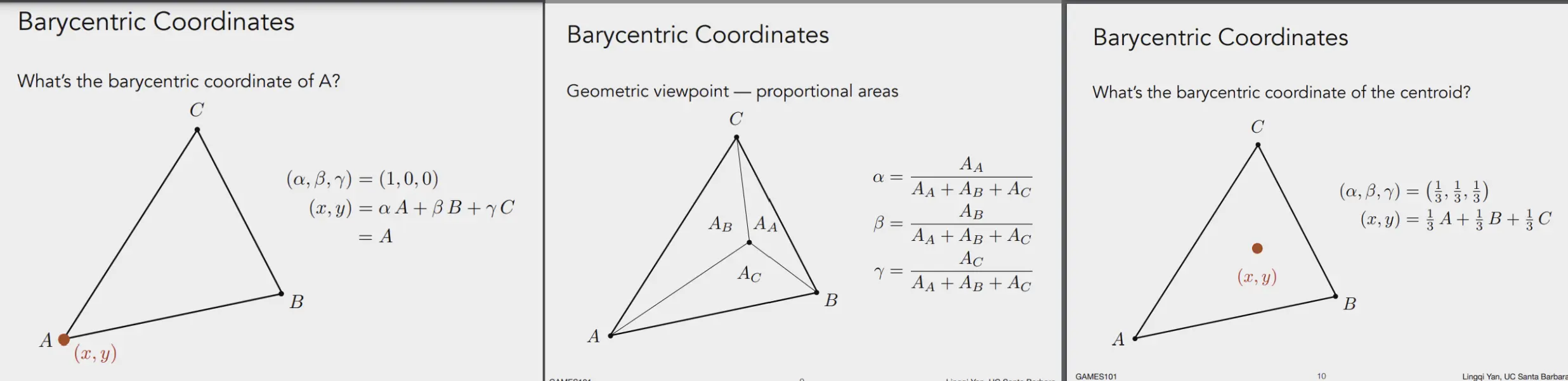
• 利用重心坐标系，就可以进行对各种基于顶点的属性，进行顶点插值

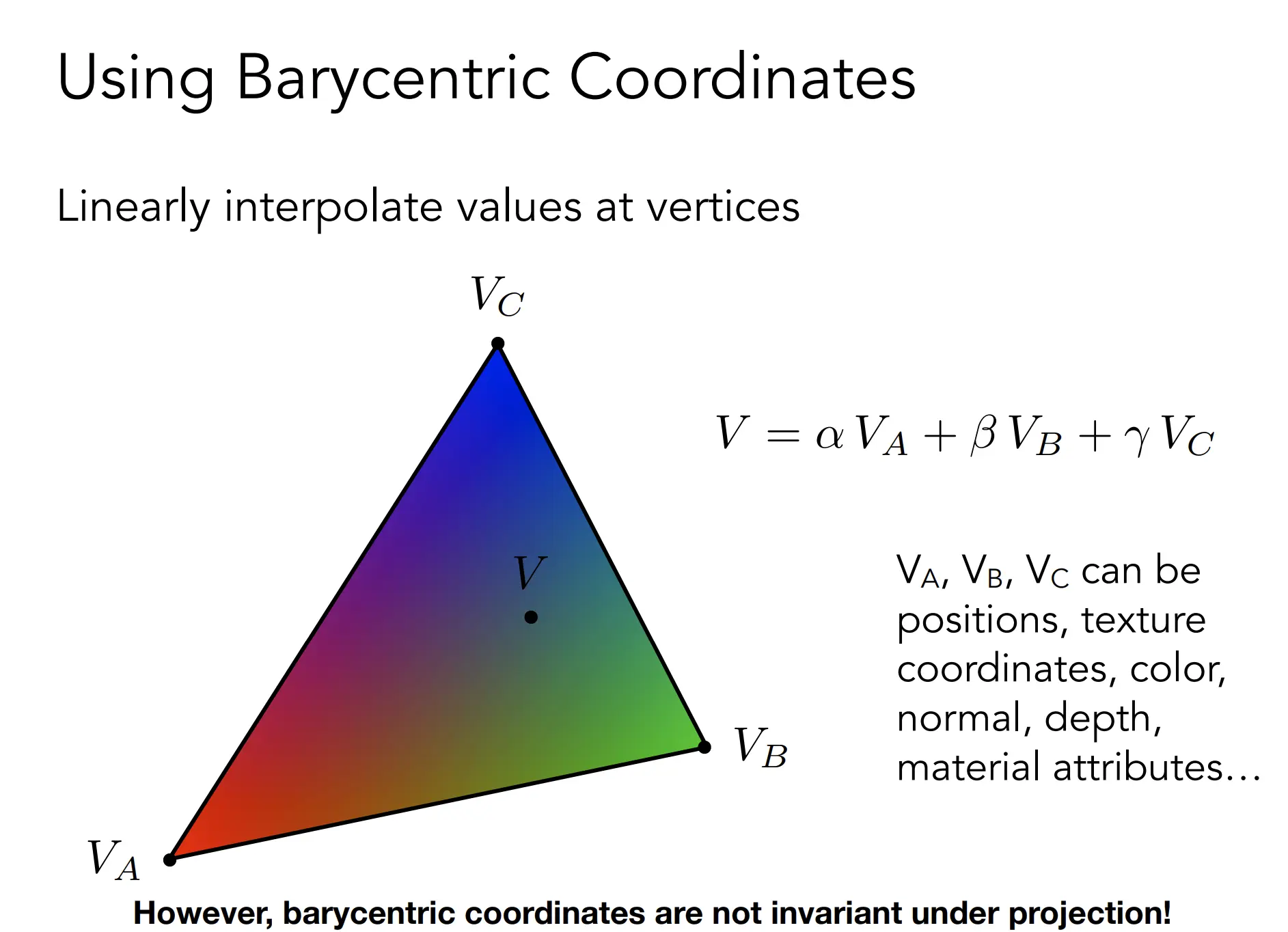
纹理映射

• 纹理，认为纹素（texels）是纹理的最小单位， 之间的距离是1；256x256的纹理，就有256x256个纹素.
• 光栅化后，屏幕像素可能会被映射到纹素之间，总之肯定不会恰好对准到某个纹素的位置。
• 为了解决这个问题，需要在纹理和像素之间进行插值，就是纹理映射。
• Nearest: 最近邻插值，取最接近的纹素的颜色，会导致明显的锯齿
• Bilinear: 双线性插值，取最接近的两个纹素的颜色，可以避免锯齿，但是会导致边缘模糊。（做了3次插值）
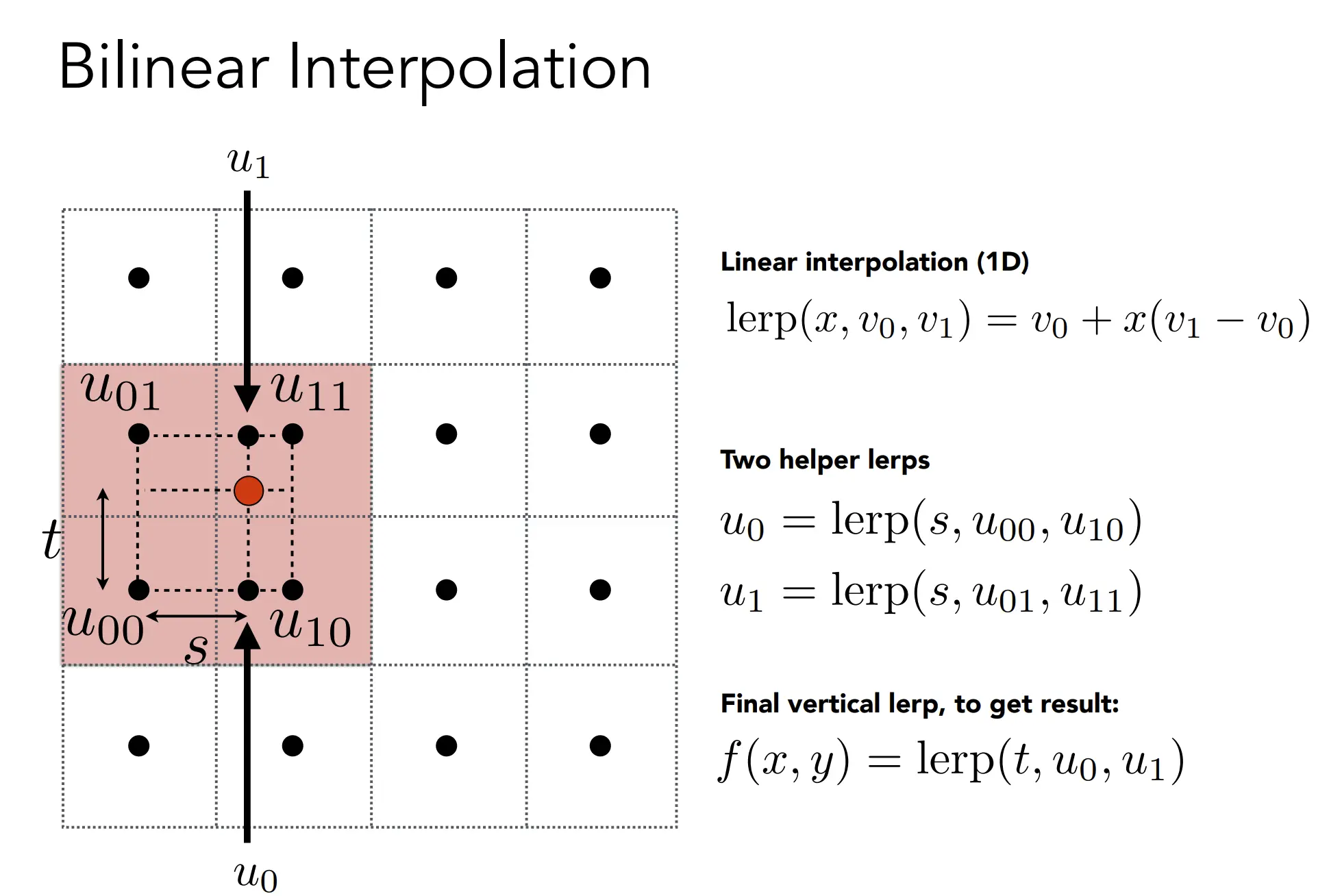
• Bicubic: 双三次插值，取更多的纹素进行插值，效果更好，但是计算量更大。

Texture Magnification

上述是纹理小，屏幕大的情况，连续的像素之间，可以利用纹素进行插值，来实现纹理的放大。 但是如果一个像素，覆盖了多个纹素，比如视角的远处，就会导致颜色错乱(Moire)。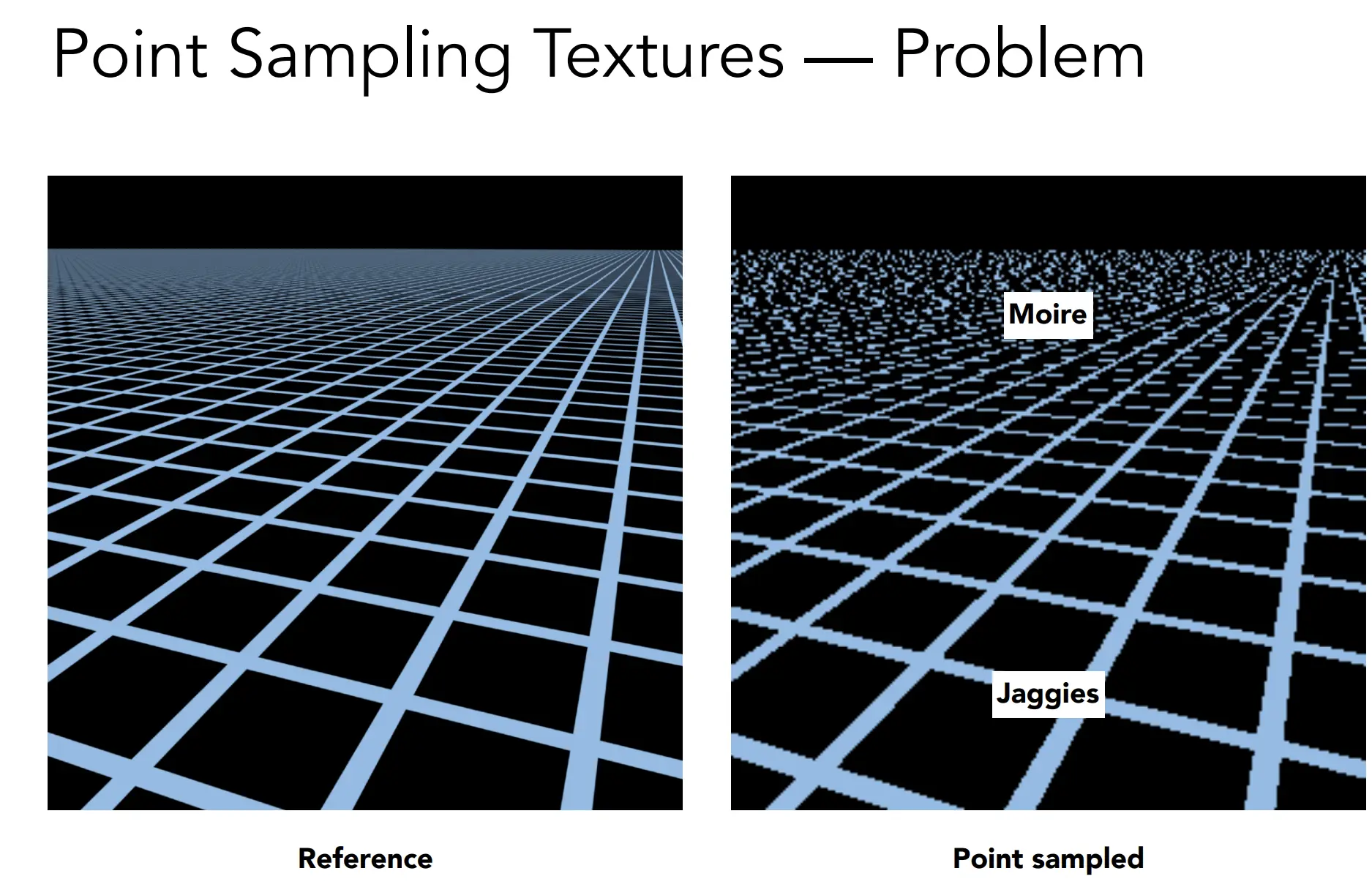

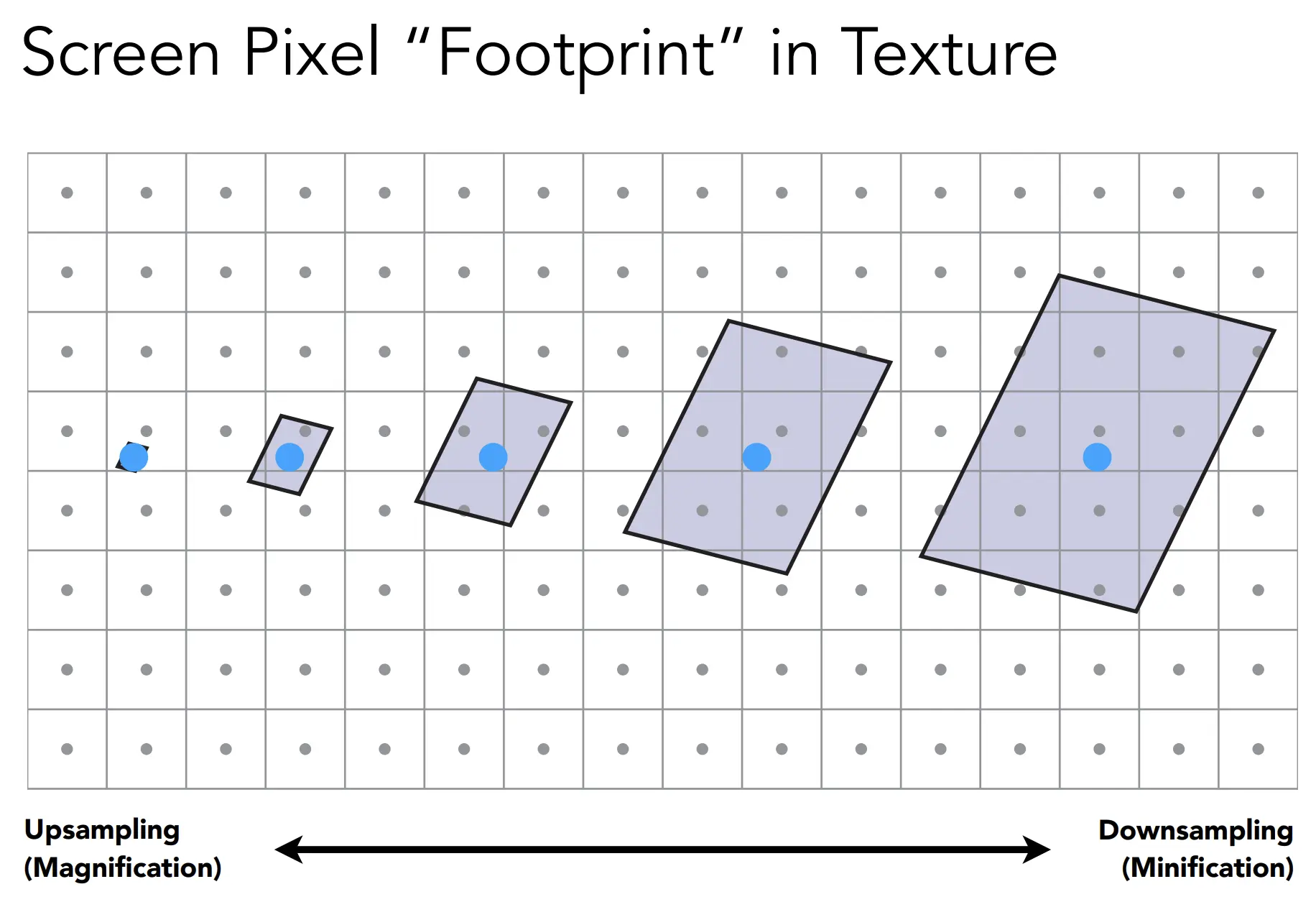
• 可以通过超采样，来解决这个问题，但是计算量会更大，效果不明显。

• 假如一个像素覆盖了4个纹素，那么就用4个纹素的颜色平均值来代替。对非常远的物体，一个像素可能覆盖全部，比如256个，计算量会特别大。

• Mipmap被设计成预计算后存起来，仅增加1/3的显存占用。每层Mipmap的尺寸都是上一层的一半，直到最后一层，尺寸为1x1。。极限求和是1/3。

• 所以Mipmap是一种查询系统，查询用哪一层Mipping作为当前像素的均值。假如覆盖了2个纹素，这些纹素之间的距离是1，那就是用最外层，原始层，也就是第0层。

• 假如某个像素覆盖了很多纹素，这会在纹理上投影出一个大点P(覆盖了很多个纹素)，那么再取邻近像素的对应的纹素大点Q，（相邻可以是上下左右）获得两个点之间最大距离L，假如L是8,就代表信息量缩小了8倍，用log2(L) 就可以知道它要用第3层Mipmap来查询均值。

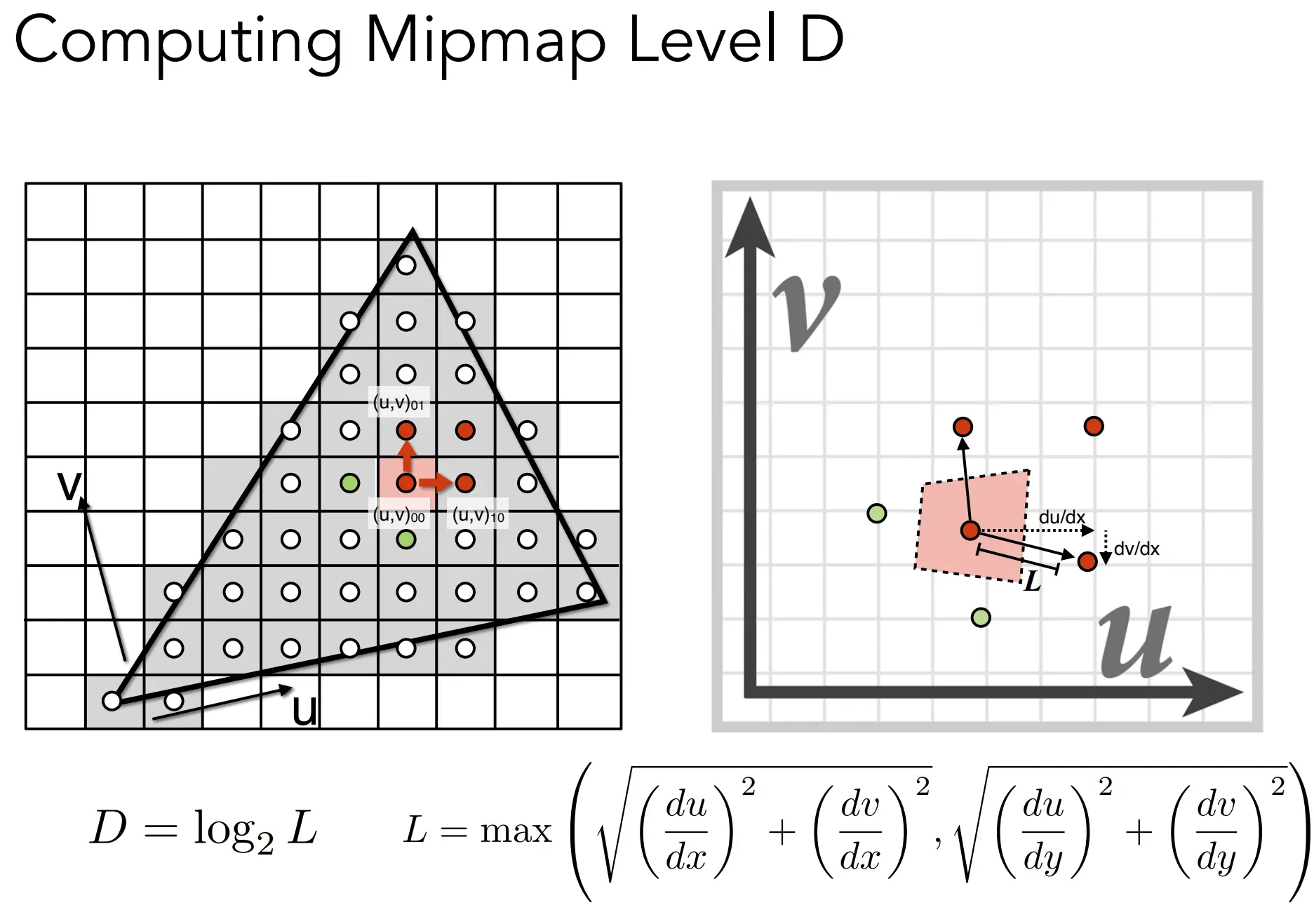
• 但还是会有锯齿问题，因为Log2(L) 的结果往往不是整数，这就需要 层与层之间进行插值。

• 这个插值叫做 Trilinear Interpolation(三线性插值) 或者 Trilinear filtering,能达成非常好的抗锯齿效果，但是计算量更大。

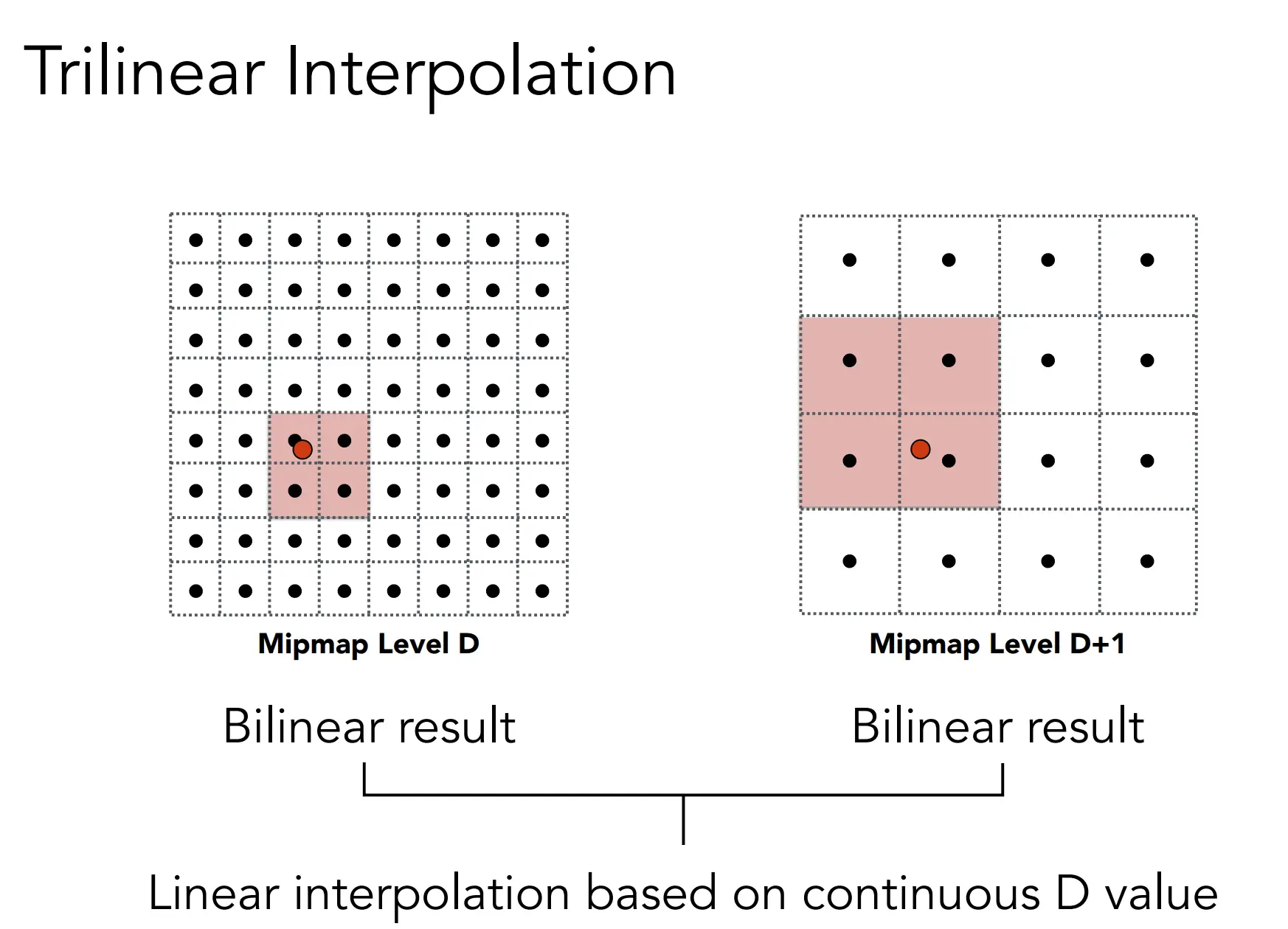
• 经过上面这些步骤，远处的位置，还是有模糊感，因为不同视角下，纹理缩小的方向是不同的，而Minimap的缩小方向是一致的，所以最终的结果就是模糊的。

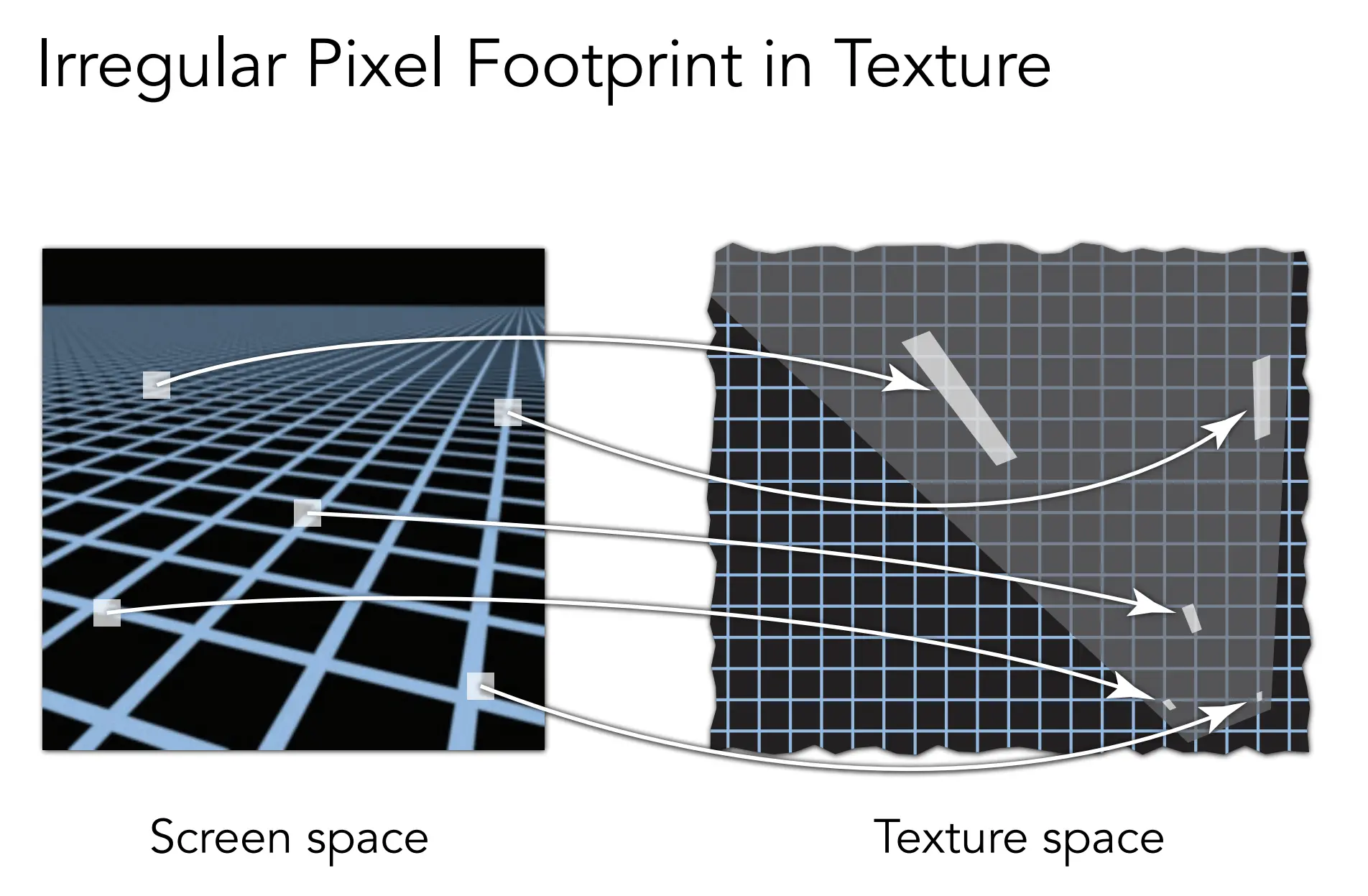
• Anisotropic Filtering(各向异性过滤)可以部分解决这个问题。图中对角线就是普通的Mipmap. 特殊实现下还是有问题。

• EWA Filtering(Exponential Weighted Average过滤)是一种更好的方法，它可以在不同的方向上进行过滤，并且能够更好地平滑纹理。计算压力较大，暂时未讲原理。

几何 (基本表示方法)

https://sites.cs.ucsb.edu/~lingqi/teaching/resources/GAMES101_Lecture_10.pdf

环境光捕捉

• 环境光可以用 镜面球来捕捉，做成Spherical Environment Map
• 但Spherical Environment Map 被处理成为 方形后，上下边缘部分有严重的拉伸。
• 为了解决这个问题，需要用Cubemap来表示，就是在反射球套上一个正方体，这样就不会出现拉伸问题了。

法向贴图，置换贴图

法向贴图可以在不增加实际几何的情况下，使用贴图来模拟更细节的表面法线，可以在低模基础上实现更平滑的光照效果，相比细分曲面，对性能影响较小

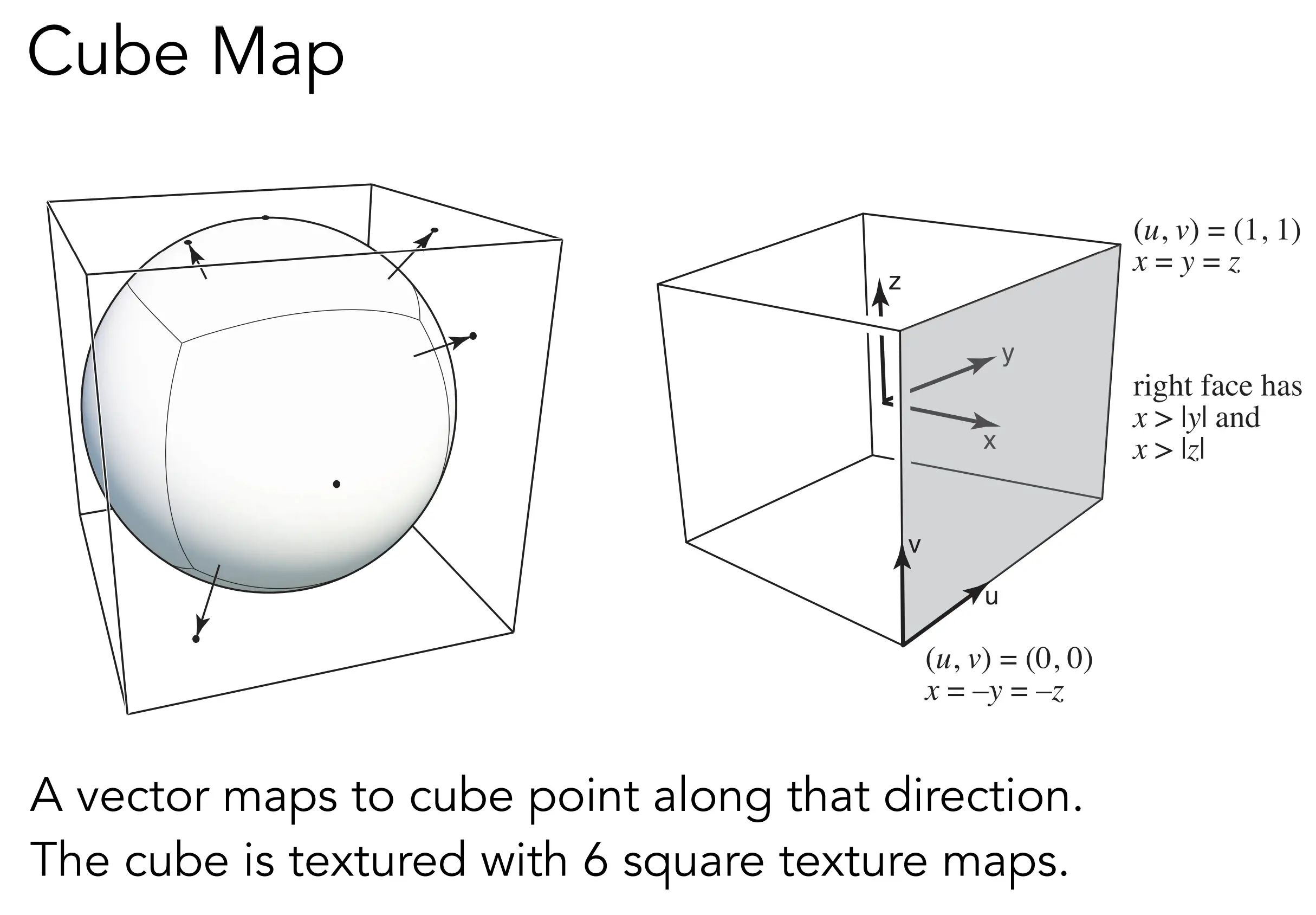
• Bump Mapping，凹凸图，用高度来影响法向的计算。

• 法向计算：微分，获得向量，V(1,dp)的垂直变换就是 N(-dp,1)。3d同理。

• Displacement Mapping，纹理置换，修改顶点来影响模型的最终展示。好处是比Bump Mapping更加真实。

• Displacement Mapping 对高模的影响更加好。

• 还有 用于程序化计算的噪声图，预计算（烘焙）的环境光遮蔽图，3d体积渲染图。

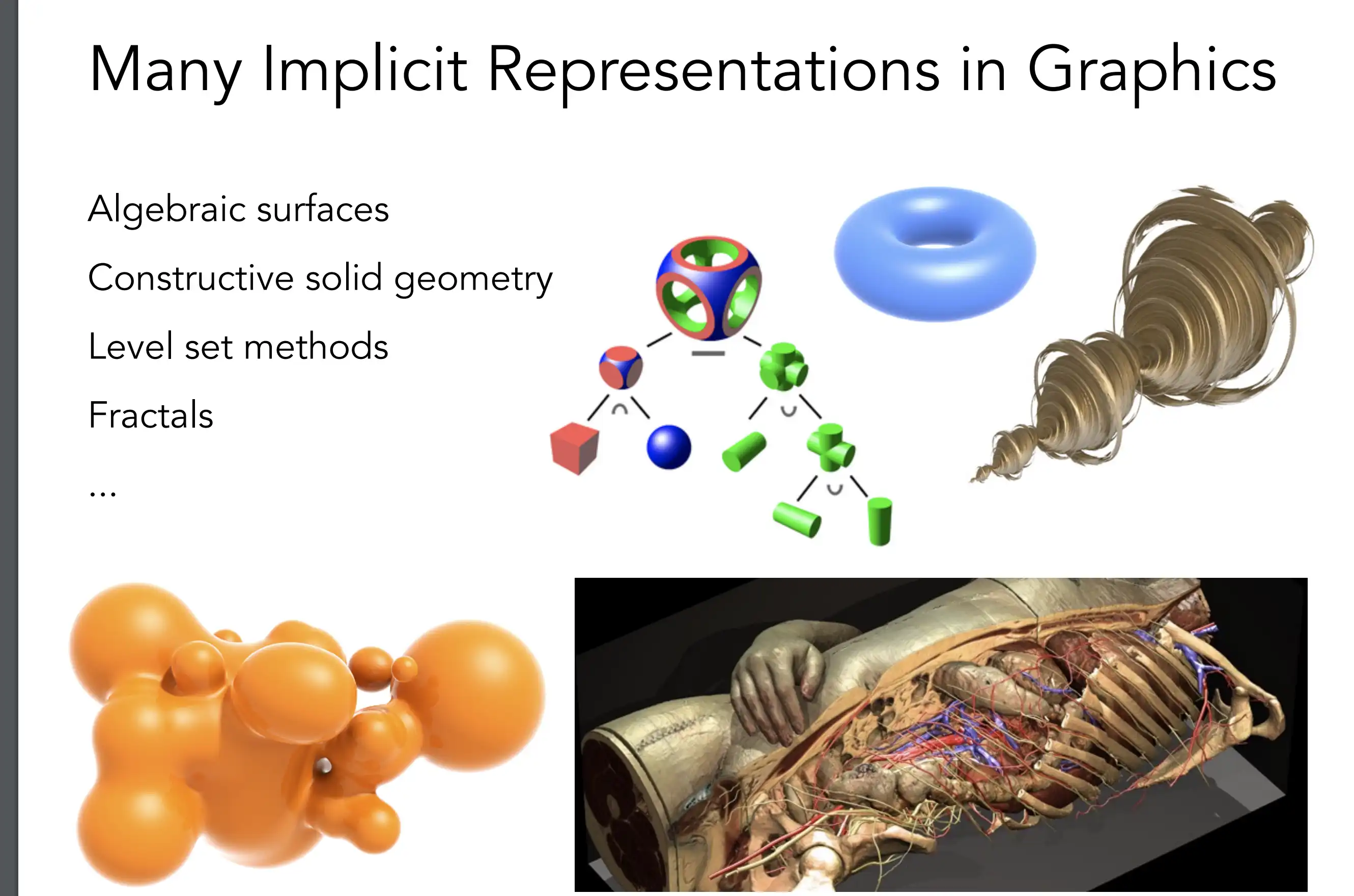
Geometry Representation

• 几何的表示，有显式和隐式的两种方式。

• 显式的表示，比如三角形，直接用三个顶点来表示。比如最常见的 Mesh。

• 隐式的表示，SDF，用一个函数来表示。

• 纹理映射，也是显示的表示，虽然看起来是函数，但值是预先记录在纹理里的，只是映射期间用了计算。（其实我觉得应该叫做半隐式的表示）

• 皮克斯高级研究人员，宣称很讨厌Meshs，它太难了。

• 布尔运算，是非常常见的隐式表示：

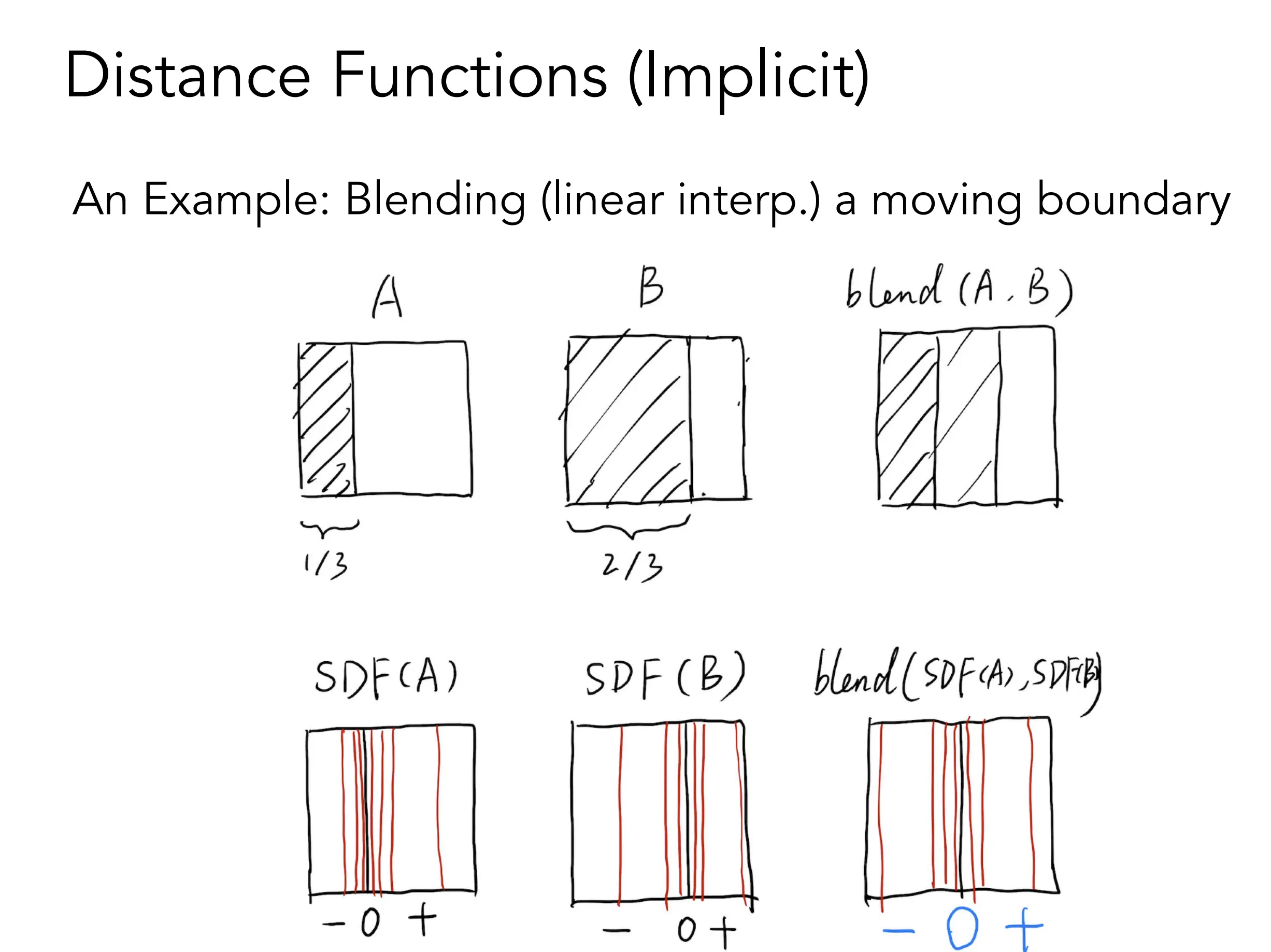
• SDF 对某些计算友好，比如混合（插值），还不占用磁盘空间，毕竟只是一个函数。图中对边界进行了插值。
  

• Level Set, fractal (没有细说)
  

wavefront OBJ 文件格式

OBJ是Wavefront科技开发的一种几何体图形文件格式。该格式最初是为动画工具Advanced Visualizer开发，现已开放，很多其它三维图形软件中都有使用。

• v 是顶点，图里是正方体8个顶点
• vt 是纹理坐标，顺序不能乱，后续面里会根据先后序号来引用。
• vn 是法向量，图里是正方体，理论上应该是6个法向量，图里出现了8个是一种数据冗余。
• f 是面，由3点组成，每个点的格式：v1/vt1/vn1，没有纹理可以写成 v1//vn1
• 可知存在纹理时，每个顶点有映射在纹理里的平面坐标。然后通过三角坐标来采样三角形内每个像素的纹理。
• 更多未提及的格式参考 维基百科 Wavefront OBJ

Bezier Curves

贝塞尔曲线

https://sites.cs.ucsb.edu/~lingqi/teaching/resources/GAMES101_Lecture_11.pdf

https://math.hws.edu/eck/cs424/notes2013/canvas/bezier.html

Curves

重点介绍了Bézier Curves，⻉塞尔曲线。最早基于de Casteljau Algorithm。各种贝塞尔曲线都 可以用 ** Bernstein Polynomials(伯恩斯坦多项式) ** 来表示，并推广到多维空间。

我的理解，de Casteljau Algorithm 是一种基于权重插值的算法。控制点代表曲线的权重（力），曲线上的每个点是所有控制点的加权平均。

• 三个控制点的例子（quadratic Bezier，二阶贝塞尔曲线）：

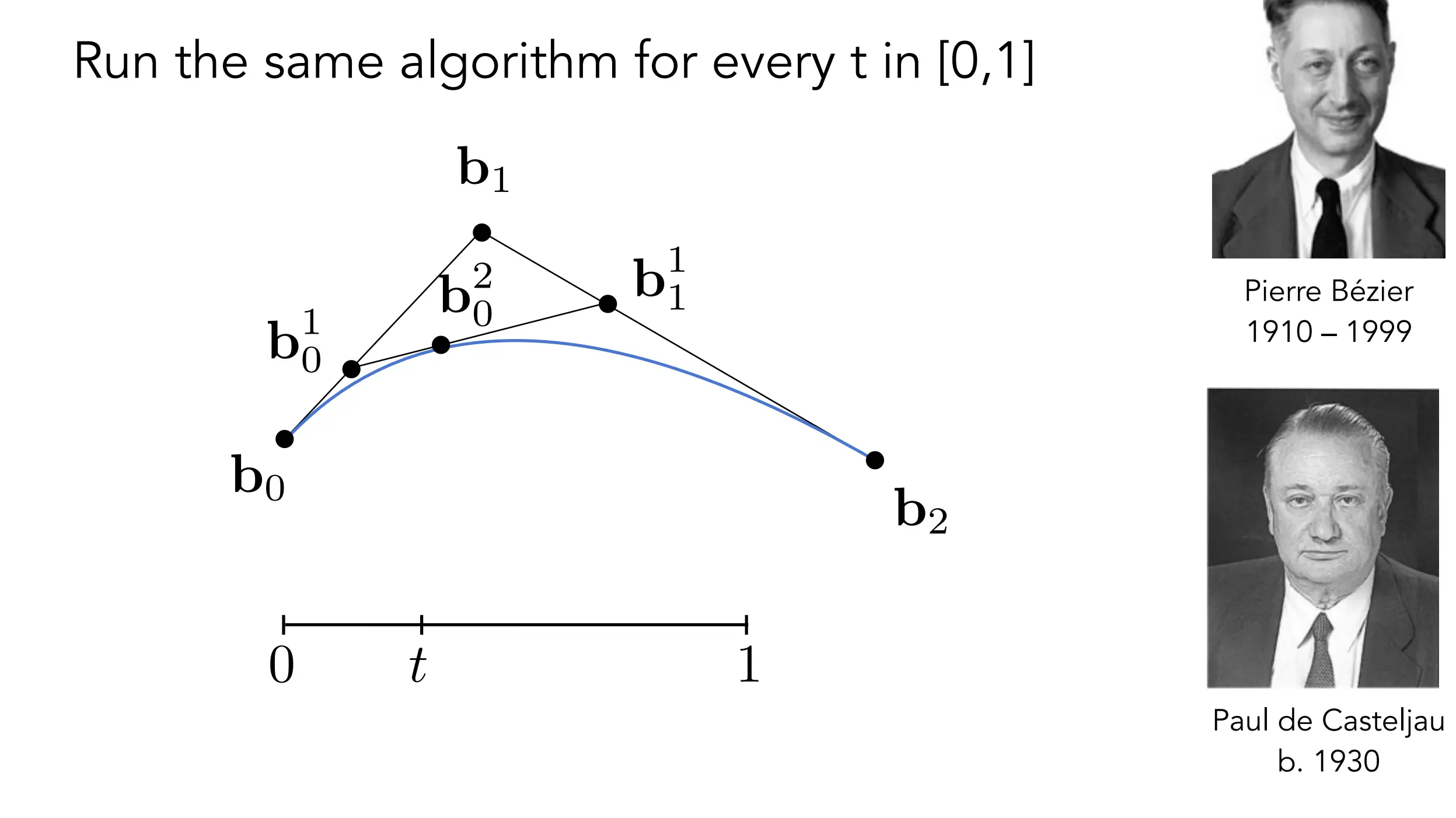
• 四个控制点的例子（cubic Bezier, 立方贝塞尔曲线））:

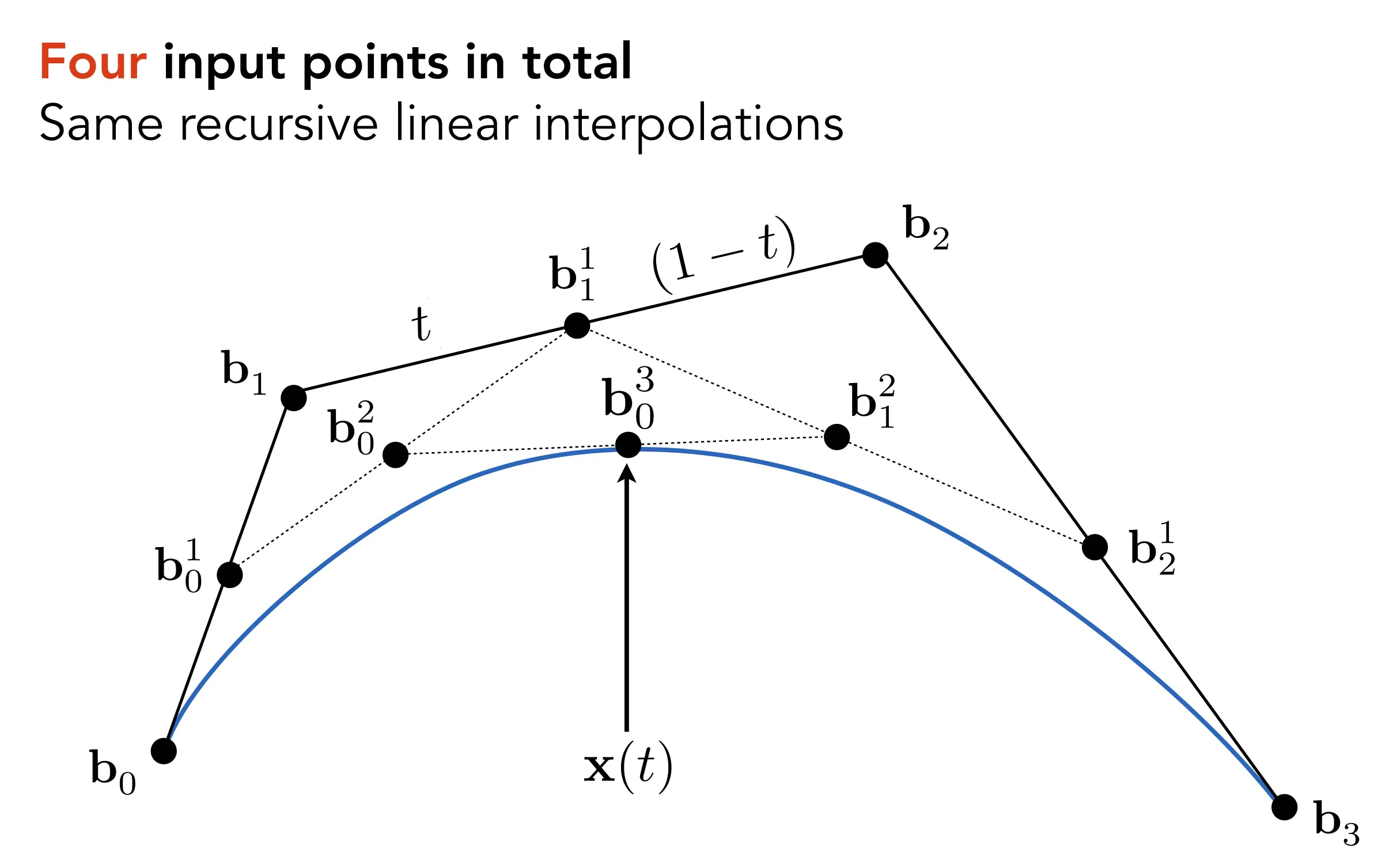
• quadratic Bezier 曲线的插值公式:

  • 有点像平方公式展开，令 1-t = x; (x + t)^2 = x^2 + 2xt + t^2
  • t取任何值，基函数之和都是1, 所以这其实又回到了重心坐标（本质上是加权平均的一种几何扩展），基函数就是每个控制点的权重。
  • 所以，Bezier 曲线上的点都必然落在构成形状的顶点的凸包内。就像重心坐标系下，所有点都在三角形内一个道理。

• 用Bernstein Polynomials(伯恩斯坦多项式)表示Bezier曲线:

  • 基函数都是连续可导，所以Bezier函数 的加权平均也是连续可导的，结果必然是曲线。
  • 特殊值，t=0时和1时，分别是起始点和终点。此时求导，方向只和相邻的控制点有关，大小是阶数。

• Piecewise Bézier Curves（分段贝塞尔曲线）

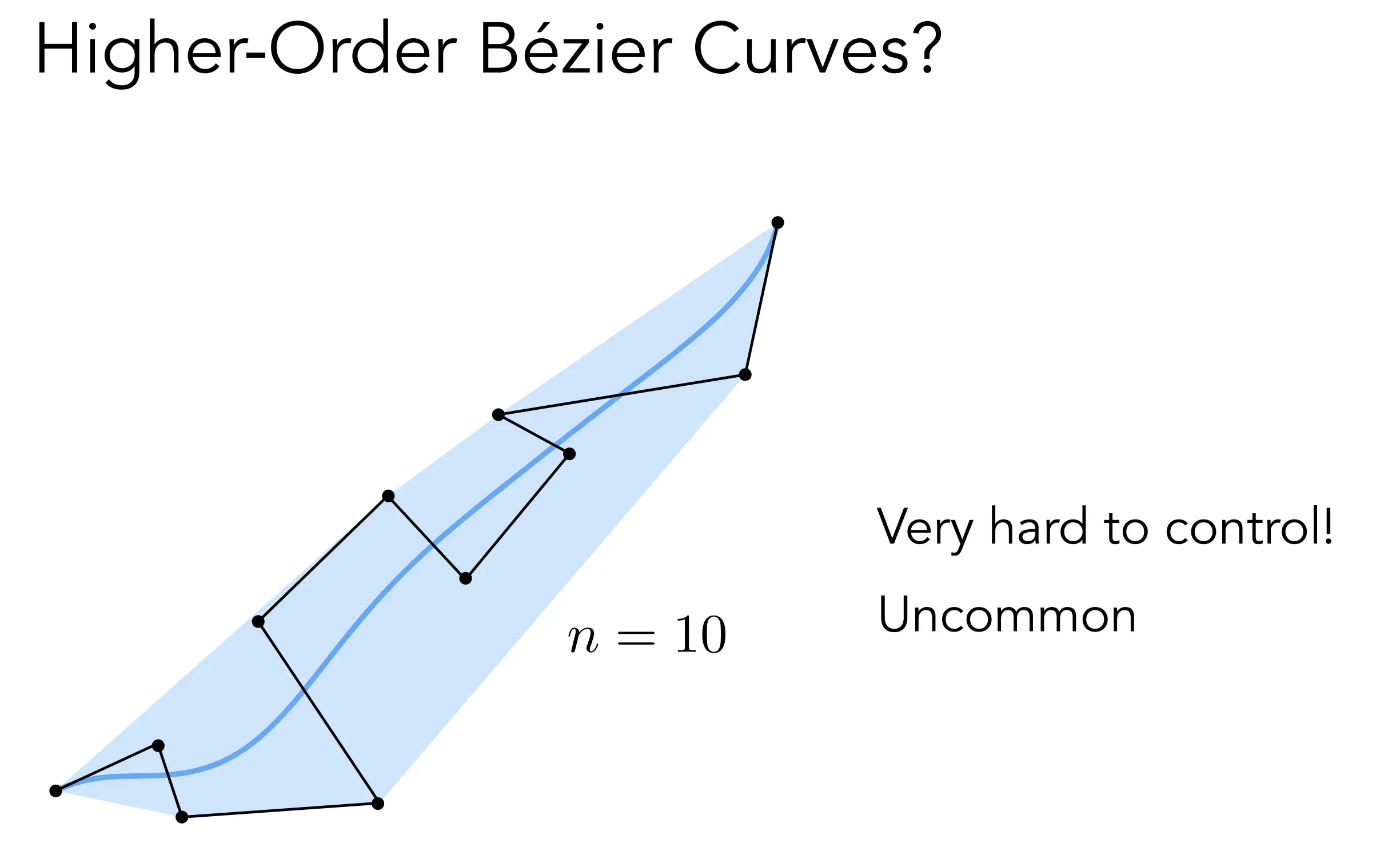
  • 由于高阶贝塞尔曲线，比如n=10，由于每个点都贡献权重，牵一发而动全身
  • 分段贝塞尔曲线完美解决了这个问题
  • 对于分段立方贝塞尔曲线的连接处，如果切线法向在一个方向上，那么称为C0 Continuity(连续性)，大小也相同，称呼为C1连续。

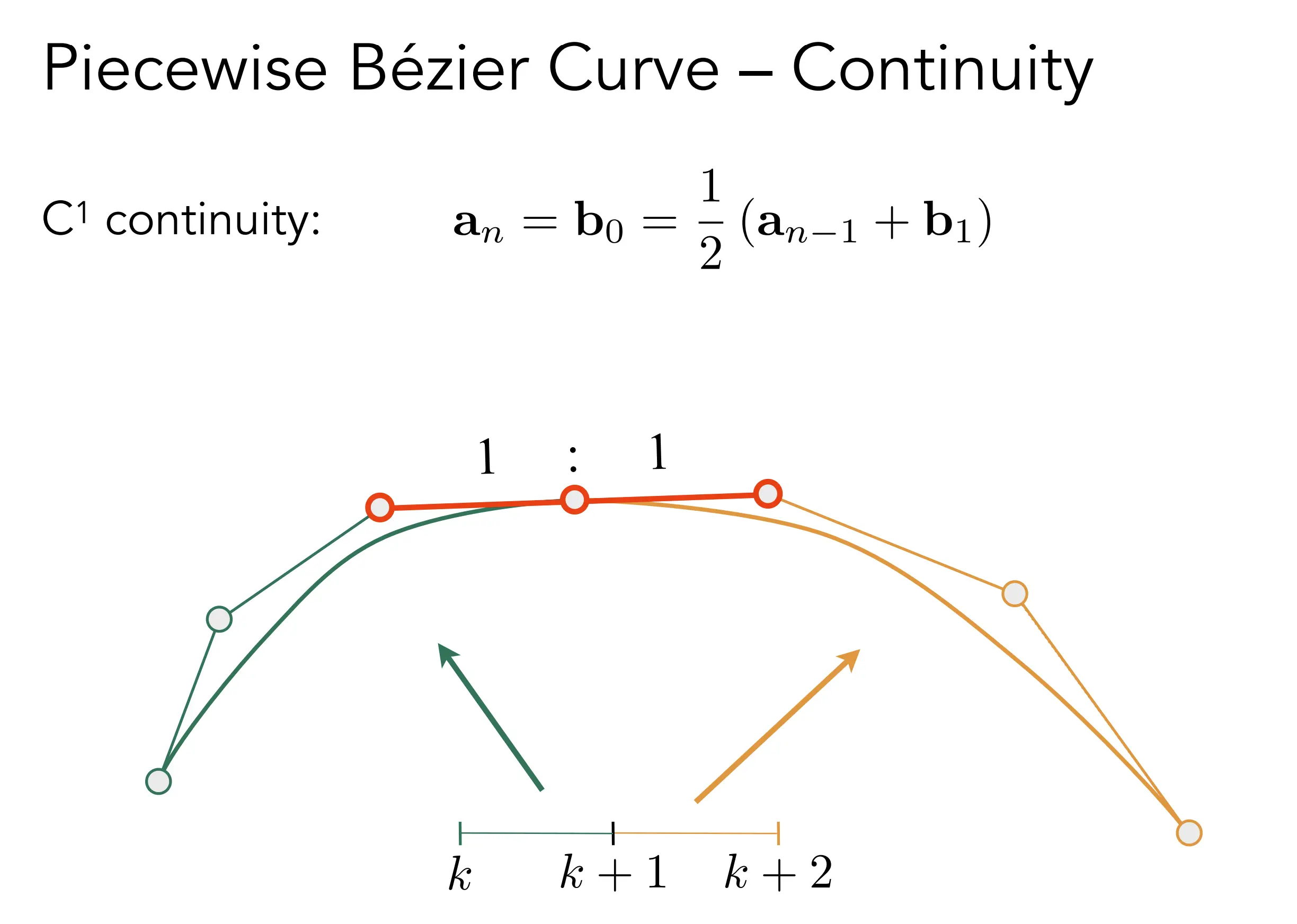
• Spline Curves(样条曲线) 可控制的曲线，没细说。

• 贝塞尔曲面

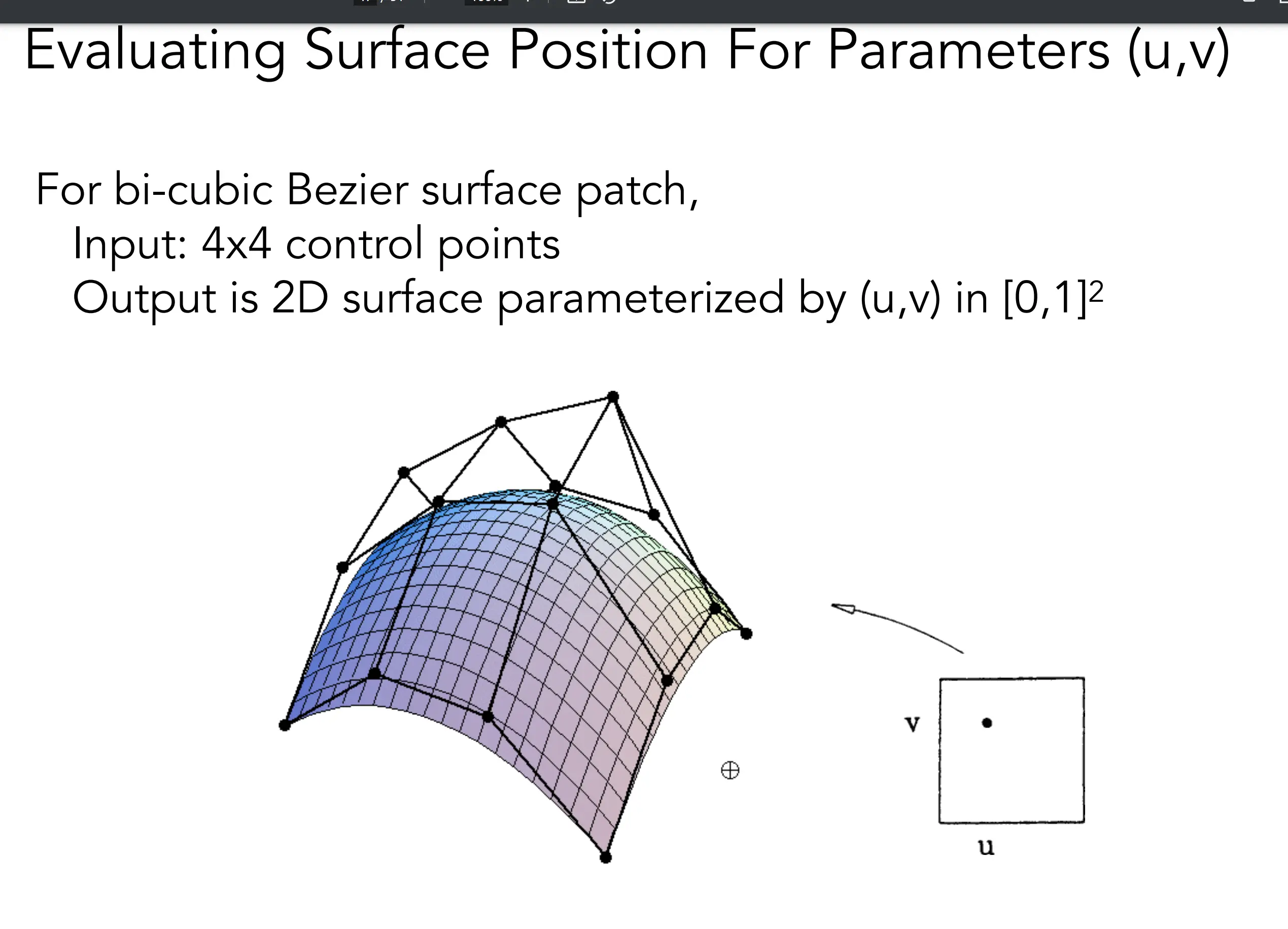
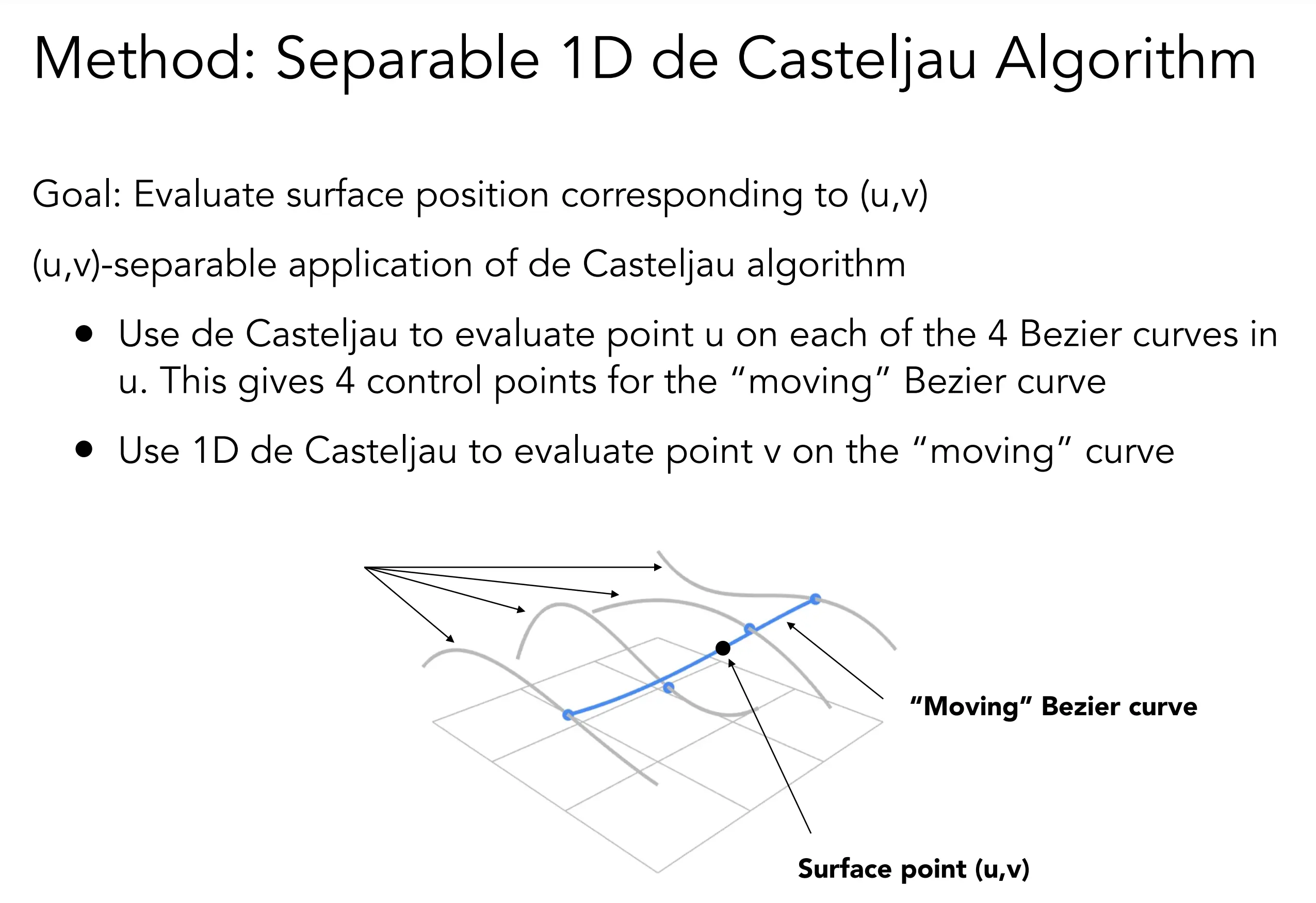
  • 原理简化版：类比二次线性插值，任意t时，各个垂直方向的点作为该方向上的控制点。

Mesh Operations: Geometry Processing

https://sites.cs.ucsb.edu/~lingqi/teaching/resources/GAMES101_Lecture_12.pdf

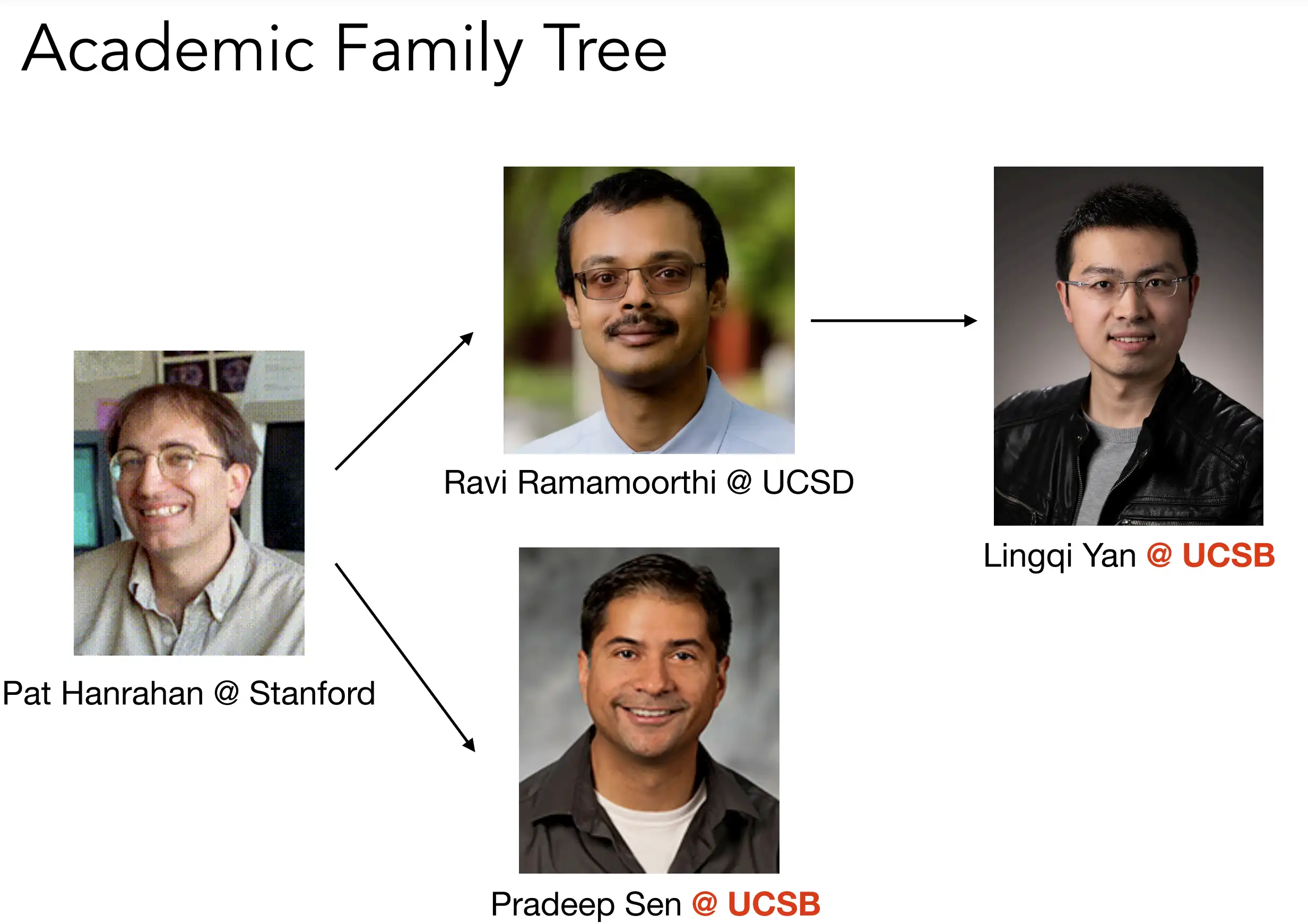
补充了一下，图灵奖获得者Pat Hanrahan，是闫令琪教授的师爷。

Mesh Regularization 正规化

• 细长的三角形不好处理，正规化处理后提高性能，但会破坏模型细节。

Mesh Subdivision

主要分两个步骤：

• 第一步，生成新的顶点
• 第二步，微调顶点的位置

Loop Subdivision (卢普细分)

• 每条边产生新的顶点
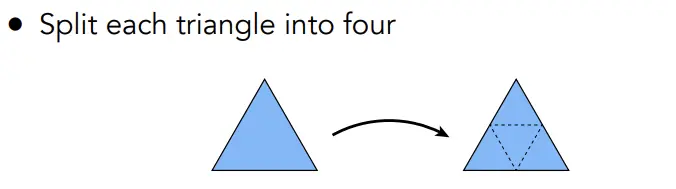
• 调整新顶点的位置，基于权重。Loop 认为，该顶点的父母（A和B）权重更大。
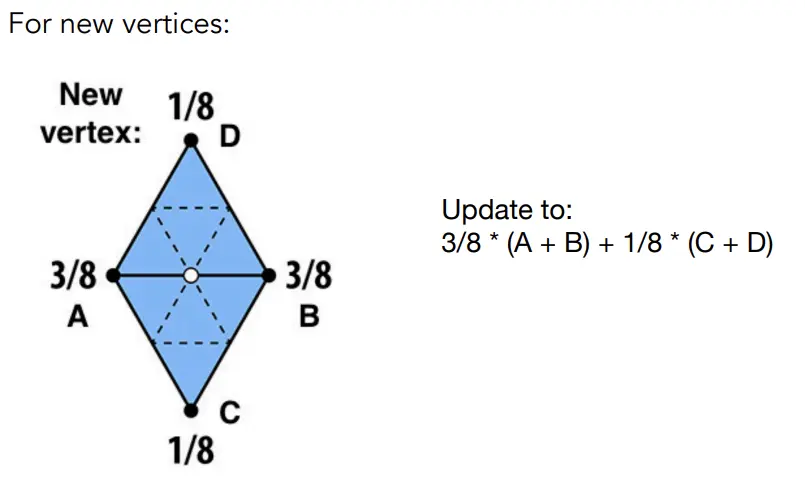
• 调整老顶点的位置，Loop 算法认为，该点的degree越大，也就是连接其他点越多，它的自身保留的权重就该越小。
• Loop 算法只能用于三角面。

Catmull-Clark Subdivision (Catmull-Clark 算法)

• 定义degree!=4的点，为奇异点。n=奇异点个数。

• 细分：每个face 添加一个新的顶点；每个edge也添加一个新的顶点。

• 观察发现，只有首次细分，会产生新的奇异点，并且个数为n

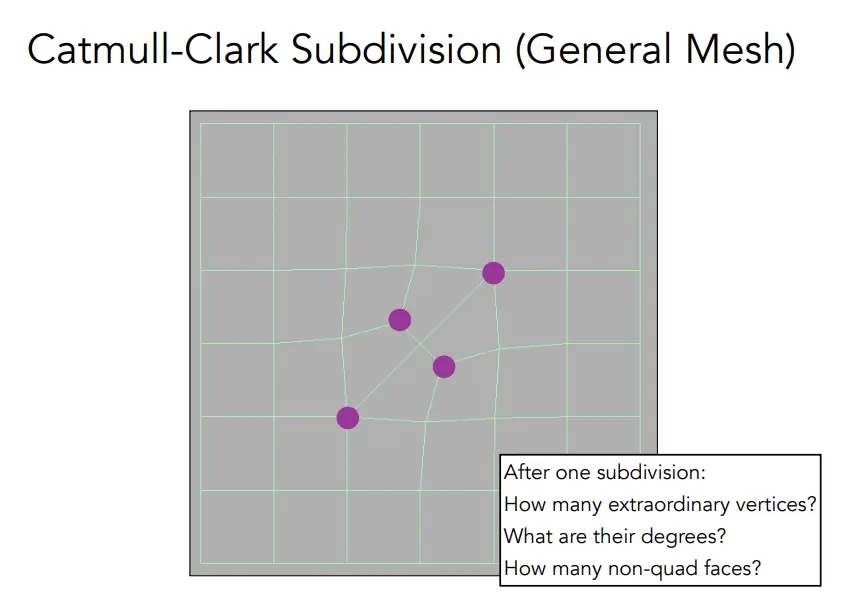
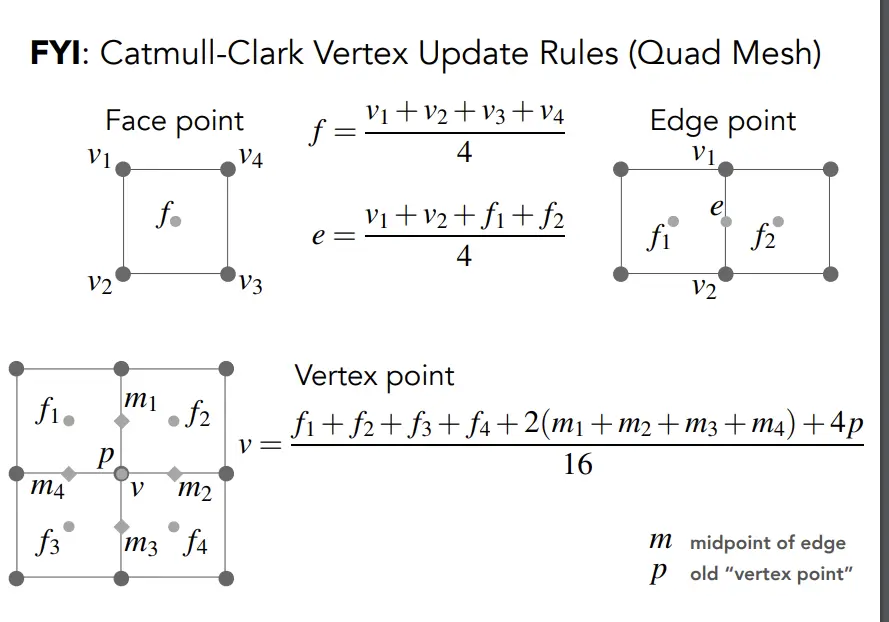
• 调整位置：新点用周围的4个相邻点的均值来调整。老点P的调整比较复杂，Catmull-Clark 认为，老点提供4倍的权重，边中心点提供2倍的权重，新点提供1倍的权重。

Mesh Simplification

• 原理是找出最小L2距离的点

Ray Tracing (光线追踪)

https://sites.cs.ucsb.edu/~lingqi/teaching/resources/GAMES101_Lecture_13.pdf

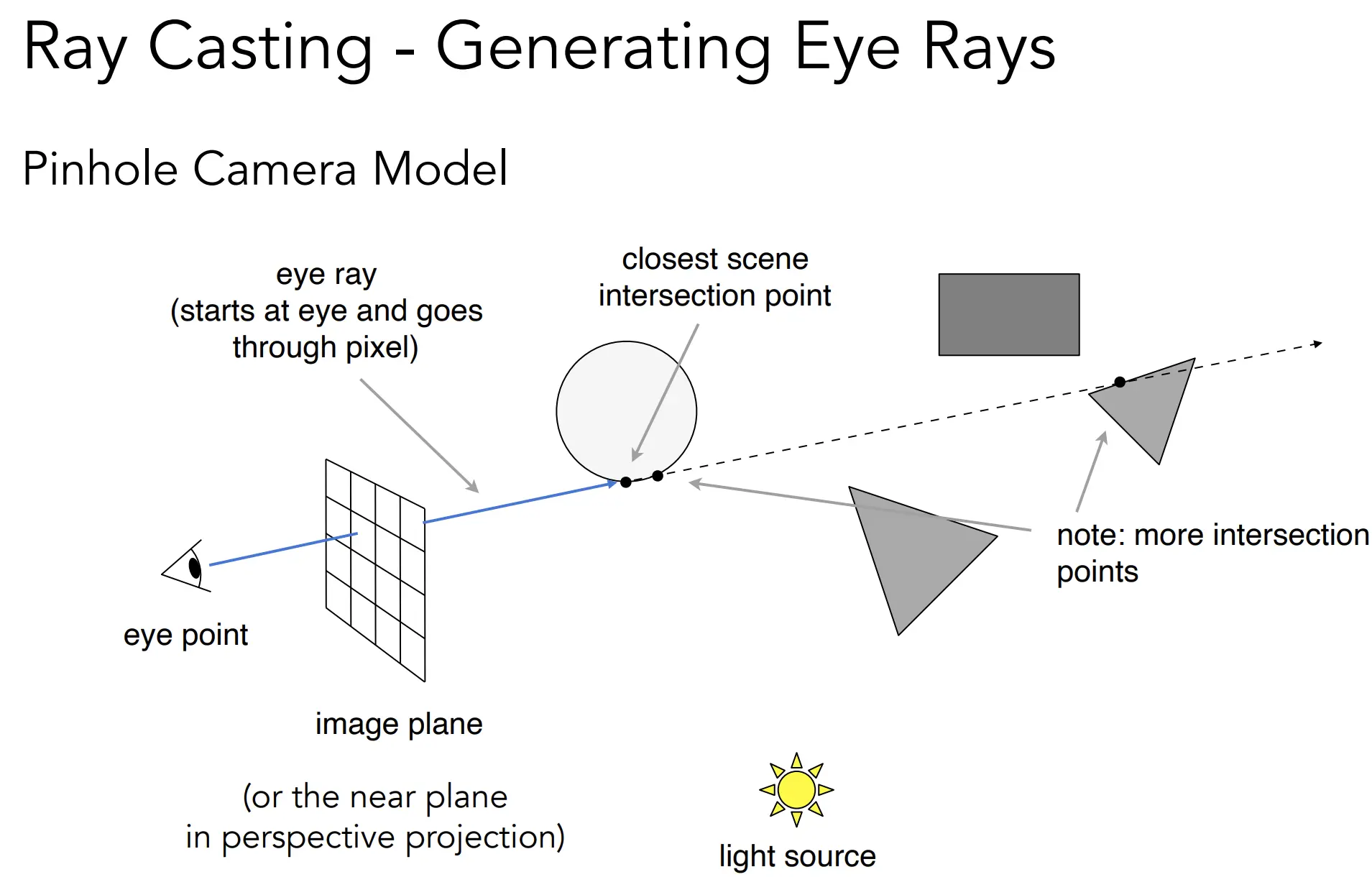
基本原理：光线走直线；光线之间不碰撞；光路可逆；

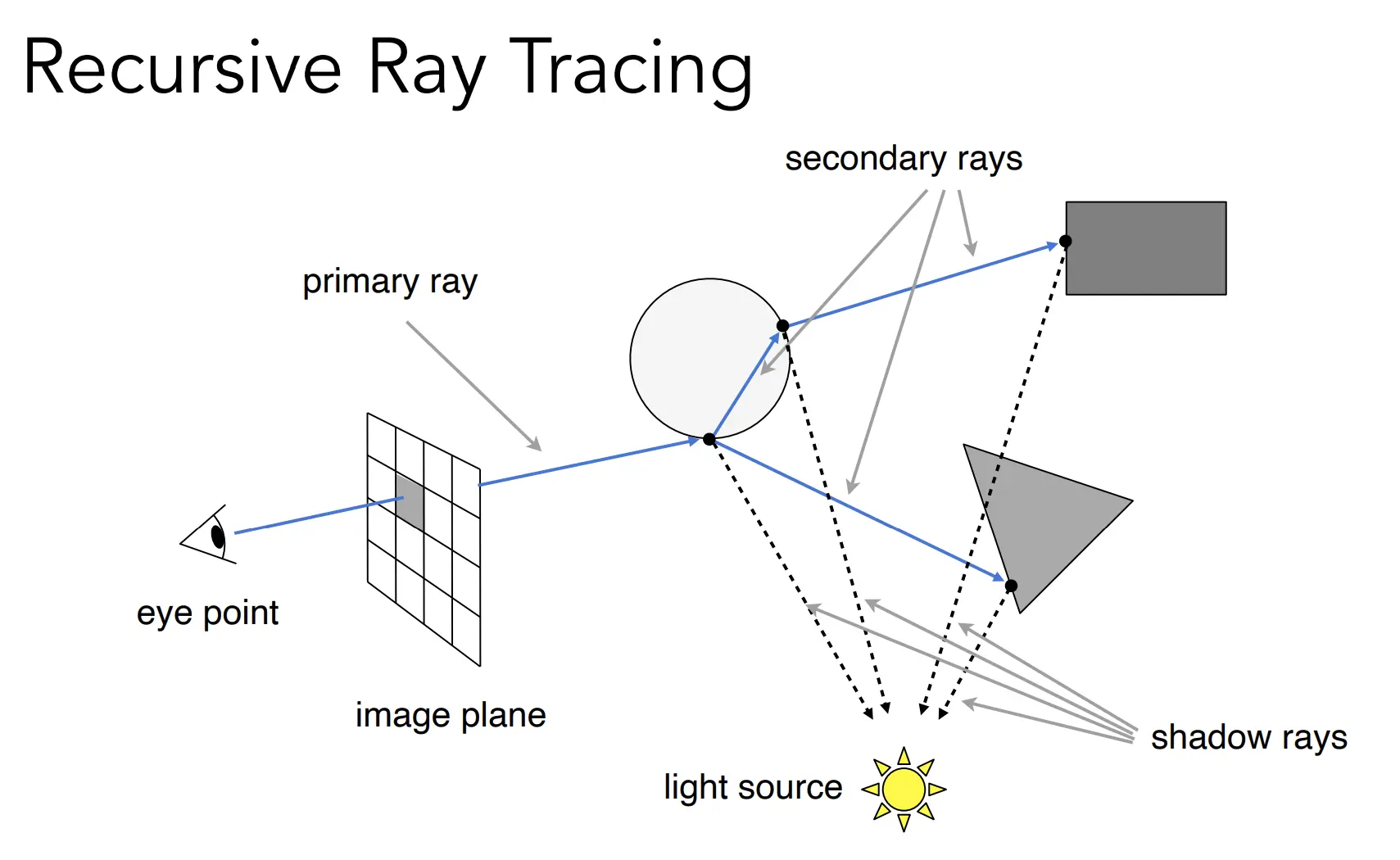
基本过程：眼睛投射光线到屏幕像素上，再到三角面的纹理点上，此时查询该点能否到达光源（连接光源），再根据着色模型给该点上色。

Recursive (Whitted-Style) Ray Tracing

“An improved Illumination model for shaded display” T. Whitted, CACM 1980

Whitted-Style Ray Tracing 是一种多次计算光路弹射后累加的光线追踪方法。

Intersection

Ray Equation (光线方程)

r(t) = o + td

• Ray Equation 用于 和 Impclict Surface Equation(隐式表面方程) 求解交点非常方便，带入即可。
• 当和显式表示如三角面求交就很不方便，因为 三角面数量太多了。

Plane Equation (平面方程)

• plane 上所有的点 和 面的法向 点乘 = 0，以此定义平面。。

Ray Intersection With Plane

• 这里N 是点乘，点乘不是乘法是算法，不能约掉，得把N乘进去再化简。

Möller Trumbore Algorithm

MT 算法，一种更聪明更快速的方法，利用三角坐标算出交点。

成本评估： 1 次除法。 27 次乘法。 17 次加法。

Details

3个未知数，3个方程 的问题，可以通过矩阵求解。

具体来说：

---

未知数

$$t,b_1,b_2$$

• $t$：光线参数，表示从光线起点 $\overrightarrow{O}$ 到交点的距离。
• $b_1,b_2$：重心坐标的两个分量（第三个分量 $1-b_1-b_2$ 自动确定）。

---

方程来源

三角形平面上的点可以用重心坐标表示，结合光线参数公式，构成以下关系式：

$$\overrightarrow{O}+t\overrightarrow{D}=(1-b_1-b_2){\overrightarrow{P}}_0+b_1{\overrightarrow{P}}_1+b_2{\overrightarrow{P}}_2$$

这实际上是 3个分量的矢量等式，即：

$${\overrightarrow{O}}_x+t{\overrightarrow{D}}_x=(1-b_1-b_2){\overrightarrow{P}}_{0x}+b_1{\overrightarrow{P}}_{1x}+b_2{\overrightarrow{P}}_{2x}$$$${\overrightarrow{O}}_y+t{\overrightarrow{D}}_y=(1-b_1-b_2){\overrightarrow{P}}_{0y}+b_1{\overrightarrow{P}}_{1y}+b_2{\overrightarrow{P}}_{2y}$$$${\overrightarrow{O}}_z+t{\overrightarrow{D}}_z=(1-b_1-b_2){\overrightarrow{P}}_{0z}+b_1{\overrightarrow{P}}_{1z}+b_2{\overrightarrow{P}}_{2z}$$

这给出了 3个标量方程。

---

矩阵形式

上述3个标量方程可以重写为矩阵形式：

$$\left[\begin{array}{ccc}{\overrightarrow{E}}_1& {\overrightarrow{E}}_2& -\overrightarrow{D}\end{array}\right]\left[\begin{array}{c}{b}_1\\ b_2\\ t\end{array}\right]=\overrightarrow{S}$$

其中：

• ${\overrightarrow{E}}_1={\overrightarrow{P}}_1-{\overrightarrow{P}}_0$：边向量1。
• ${\overrightarrow{E}}_2={\overrightarrow{P}}_2-{\overrightarrow{P}}_0$：边向量2。
• $\overrightarrow{D}$：光线方向。
• $\overrightarrow{S}=\overrightarrow{O}-{\overrightarrow{P}}_0$：光线起点到三角形一个顶点的向量。

这是一个 $3\times 3$ 的线性方程组，用矩阵表示为：

$\mathbf{A}\mathbf{x}=\mathbf{b}$

其中：

• $\mathbf{A}$：系数矩阵。
• $\mathbf{x}=\left[\begin{array}{c}{b}_1\\ b_2\\ t\end{array}\right]$：未知数。
• $\mathbf{b}=\overrightarrow{S}$：常数项。

---

矩阵有解的条件

矩阵有解的充要条件是系数矩阵 $\mathbf{A}$ 的行列式不为零（即 $det(\mathbf{A})\ne 0$）。在几何上，这意味着：

1. ${\overrightarrow{E}}_1,{\overrightarrow{E}}_2,-\overrightarrow{D}$ 必须是线性独立的。
2. 物理意义上：光线不能与三角形平行，且三角形必须是非退化的。

如果满足这些条件，就可以通过矩阵求解直接得到 $b_1,b_2,t$。

---

解法步骤

1. 计算系数矩阵 $\mathbf{A}$： $\mathbf{A}=\left[\begin{array}{ccc}{\overrightarrow{E}}_1& {\overrightarrow{E}}_2& -\overrightarrow{D}\end{array}\right]$
2. 用逆矩阵法（或高斯消元法）求解： $\mathbf{x}={\mathbf{A}}^{-1}\mathbf{b}$

Ray Tracing 加速结构

Bounding Volumes

基本思想，如果光线不和包围盒相交，就更不可能和盒内Objects(三角形)相交，用包围盒计算来减少计算量。

• Axis-Aligned Bounding Box (AABB),既 轴对齐包围盒。
• 轴对齐包围盒的好处是，不用算点乘。
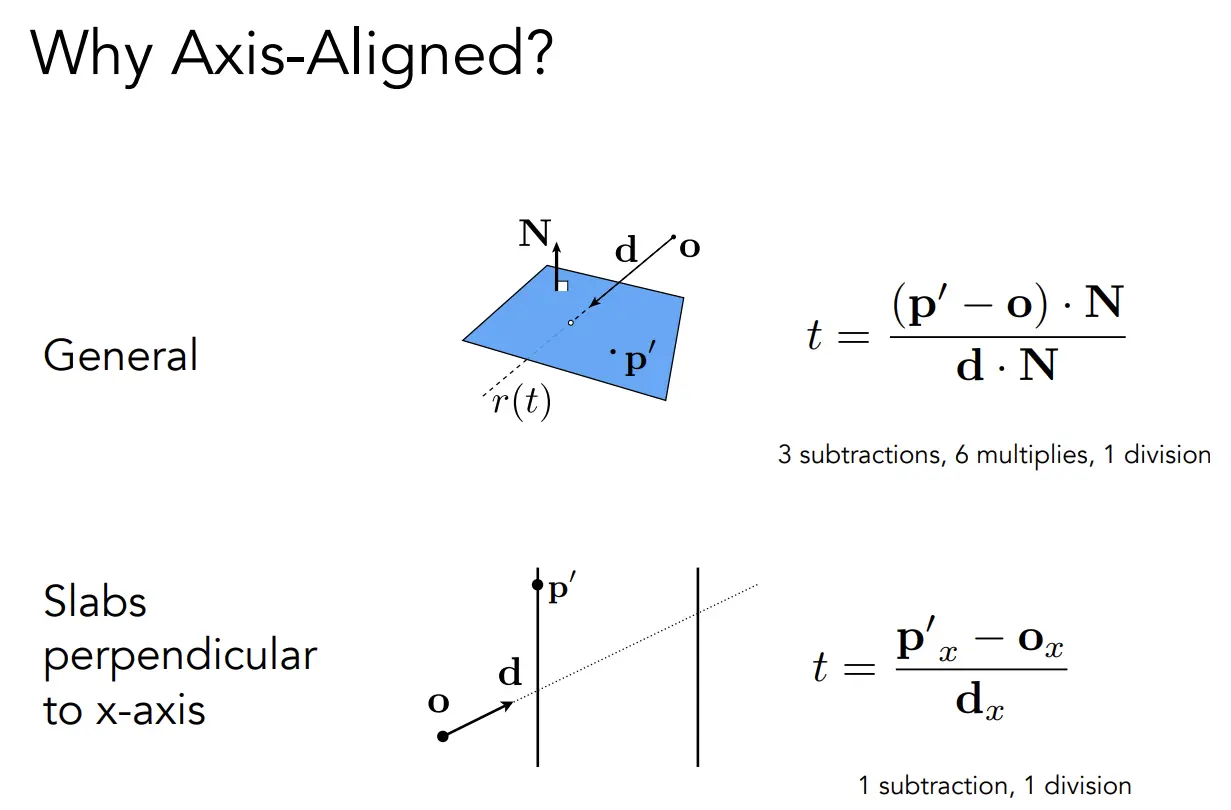
• 轴对齐包围盒的面是无限大的。
• “光线进入盒子仅当它进入所有的 slabs” 是一个 前提条件,排除了平行的可能。
• 那么，假定盒体上的面是“真面”，延长部分是“假面”。光线进入阶段，如果存在多次碰撞，那只有时间最大的那个才是真正触碰到真面。
• 而光线离开阶段，如果存在多次碰撞，那么时间最小的那个就是离开真面。
  
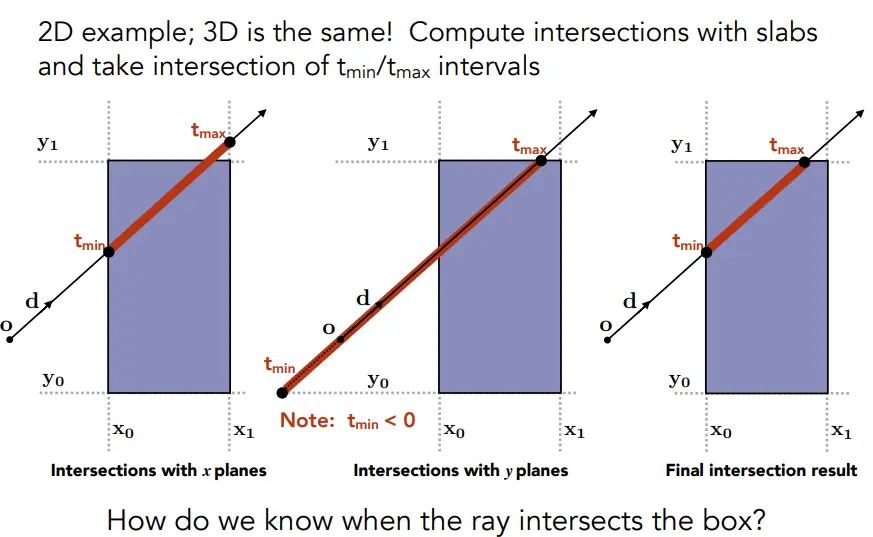
• 补充，平行的情况，需要额外的判断代码,比如：ray.origin[i] < aabb.min[i] || ray.origin[i] > aabb.max[i]

AABB 包围盒加速方案

对包围盒内部在进行细分

Uniform Grids (均匀网格，或者说体素化)

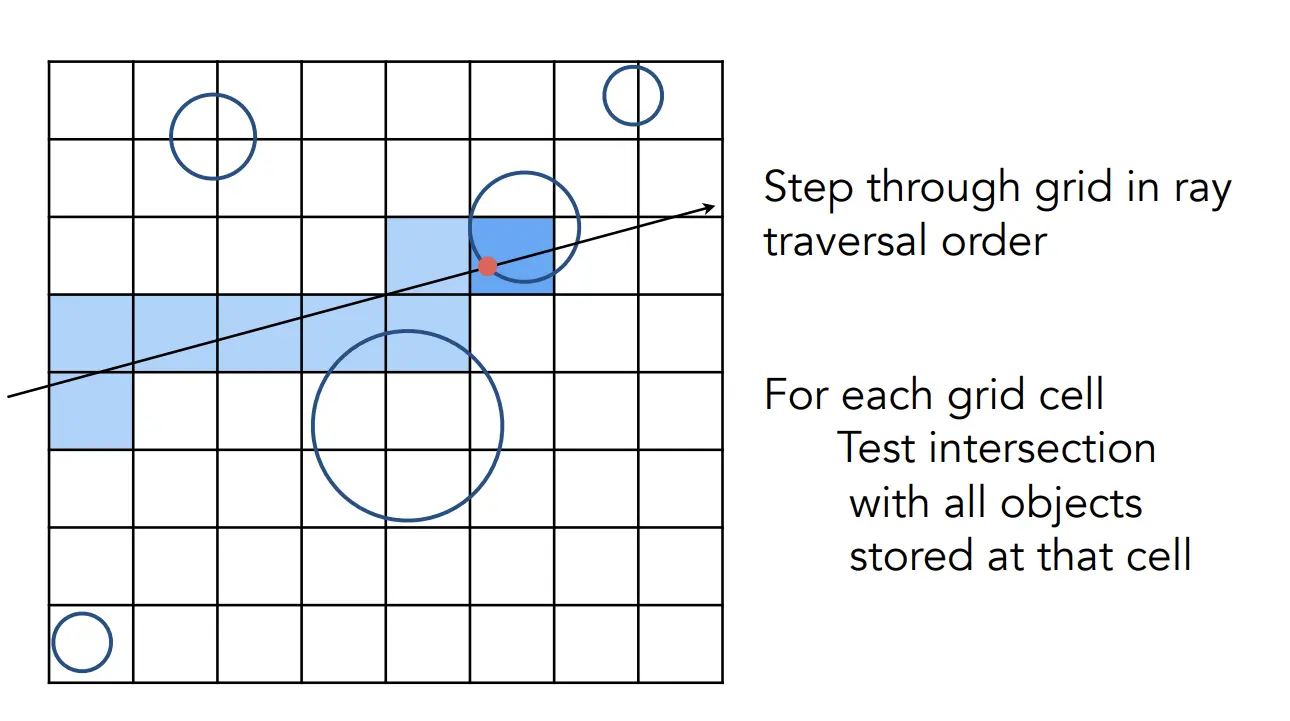
• 把AABB划分成小格子，每个光线穿过的格子，都对cell内的三角形进行求交运算。
• 格子的数量太多太少都会影响效率，需要做平衡，课程里建议是:$$cells=C\times objs$$$$C=27$$

Spatial Partitions (空间划分，或者说分块)

Grid 对于特别空旷的场景，比如 “Teapot in a stadium” problem，效果不好，所以需要用 Spatial Partition。

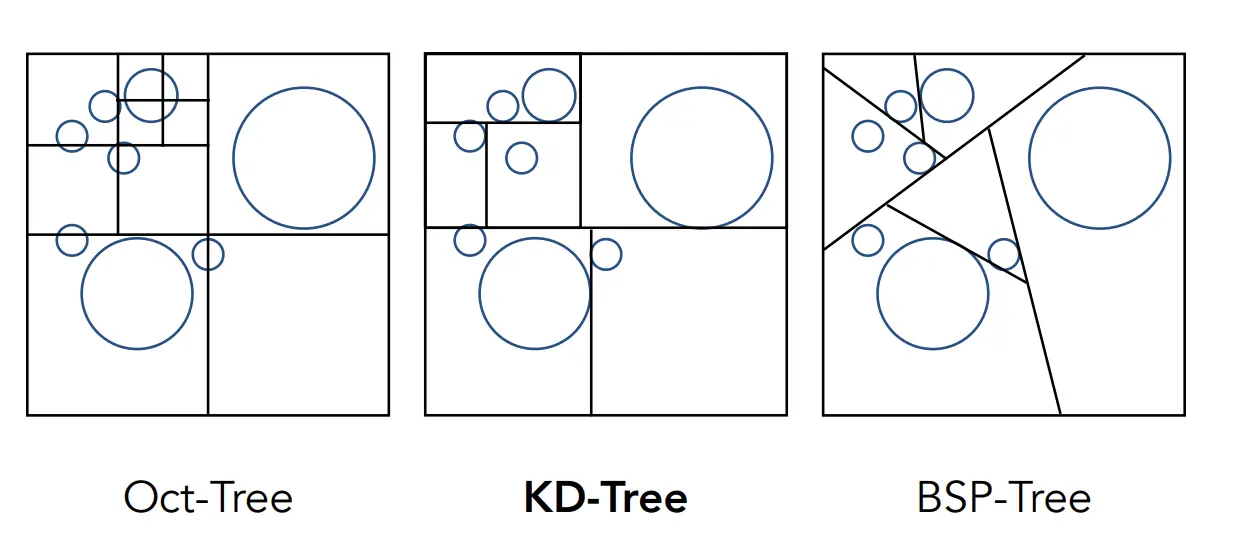
• Oct-Tree （八叉树），在空间中划分，每个节点有8个子节点。(二维是用四叉树，三维是用八叉树)

  • 只适用于3d空间
  • 无法对数据分布进行调整，不均匀，某些部分可能产生大量深层的子节点，导致影响性能。
  • 适用于本身均匀分布的数据。

• KD-Tree（k-分树），在空间中划分，每个节点有2个子节点, 是一种二叉树。

  • 适用于任何维度
  • 递归，交替地选取空间轴进行划分，是数据分布更均匀。
  • 低维空间（特别是2D或3D）的范围查询或最近邻搜索。

KD-Tree 加速原理

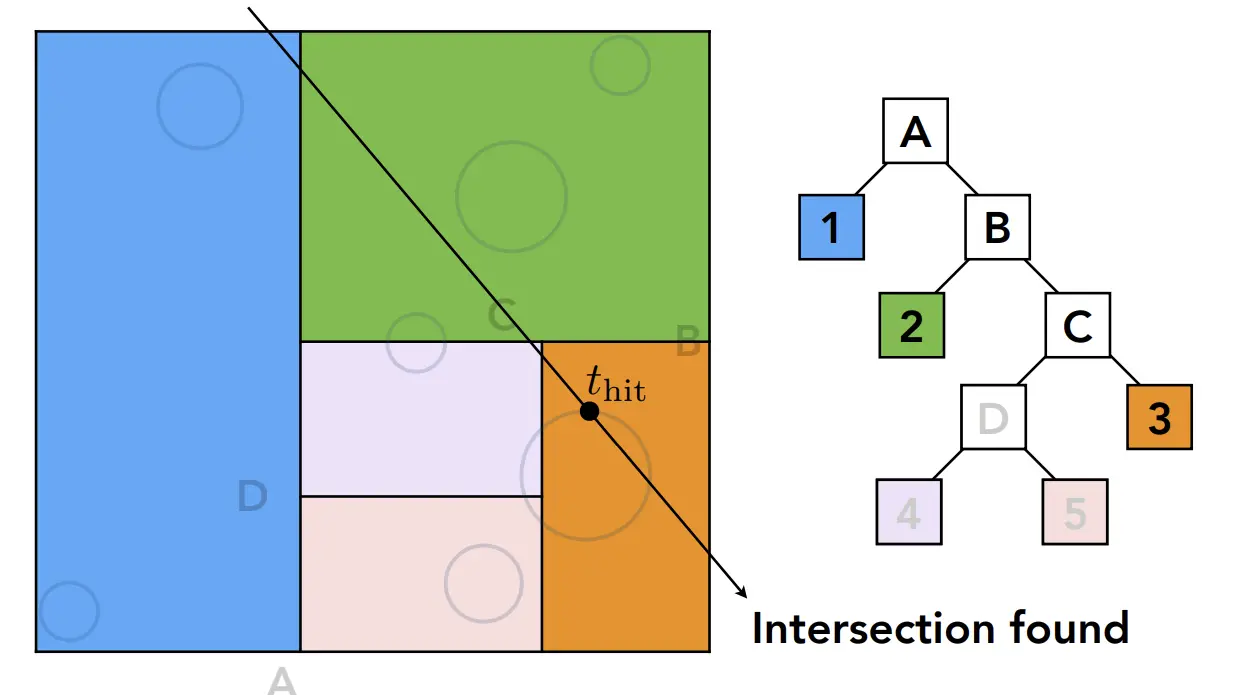
• 检查光线与AABB根节点是否被光线穿过，否则直接退出。
• 如果光线穿过了根节点，就递归地检查每个被光线穿过的子节点，直到找到 intersection.
• 优先访问靠近光线起点的子节点，减少无效检测.
• 配合 MT 三角坐标算法，在叶节点进行全部求交计算。
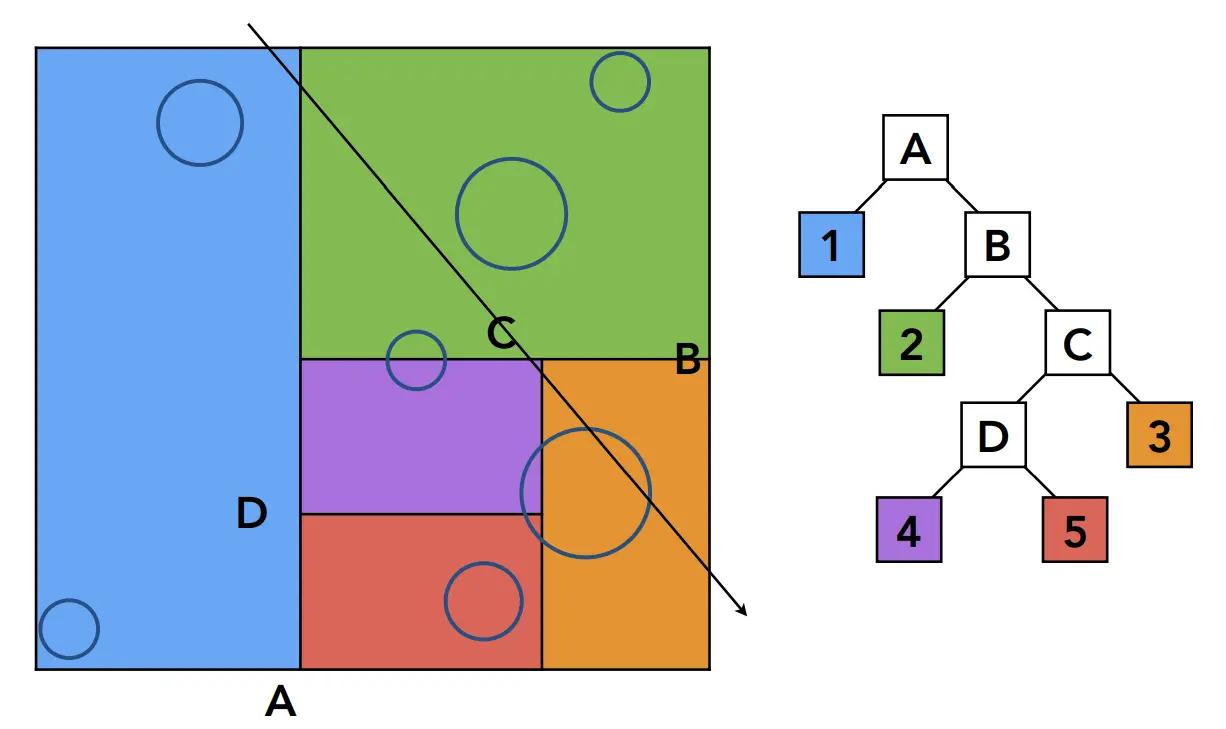
  • 图中是最坏的情况，基本上每个叶节点都需要计算，而且有很多重复计算。（objects 既在4，也在5）

Bounding Volume Hierarchy (BVH, 层级包围盒)

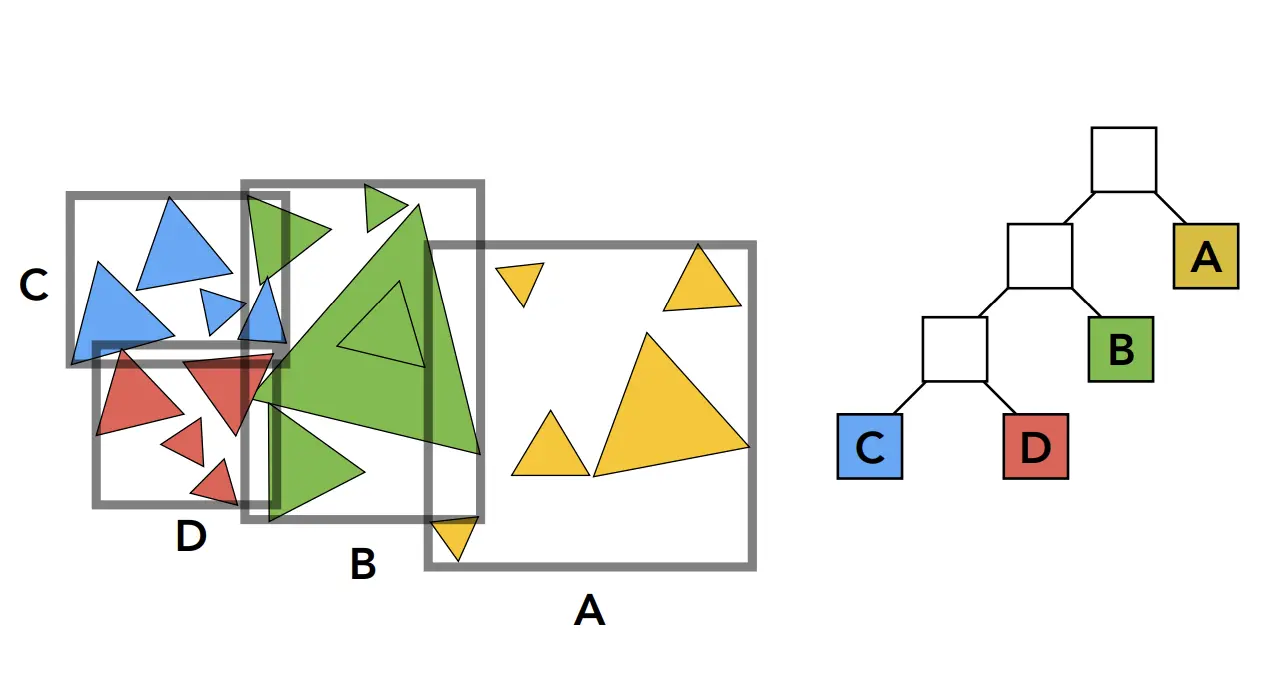
为了解决KD-Tree 的问题，存在重复检测的问题，所以引入了BVH, 是对KD-Tree的改进

• BVH:物体划分, KD-Tree: 按空间划分
• 我的理解，本质上还是KD-Tree，不同的是划分方法不同。
• BVH 从自身出发，递归地给三角面进行分组,构建子Cell空间。
• BVH 允许Cell的空间互相重叠，但内容只在其一。

Basic Radiometry (辐射度量学)

为了更好地解决 Blinn-Phong model 里 光线强度单位的问题，引入了基本辐射度量学的概念。

圆的周长：$2\pi r$

球的面积: $4\pi r^2$

角度可以表示为弧长和半径的比值：$\theta =\frac{l}{r}$，也就是弧度，当l越接近$2\pi r$ 时，角度越接近$2\pi$, 实际上就是把0到1映射到0到$2\pi$

除以半径而不是周长，是为了映射到2π

$p$: 占比，权重

$l=2\pi r\times P$

$\theta =\frac{l}{r}=\frac{2\pi r\times P}{r}=2\pi \times P$

同理，立体角也可用小面积和半径平方的比值来确定。

$\theta =\frac{A}{r^2}=\frac{4\pi r^2\times P}{r^2}=4\pi \times P$

因此：

一个完整的圆周长为 $2\pi r$，所以一个完整的圆对应的角度是 $2\pi$ 弧度

一个完整的球面积为 $4\pi r^2$，所以一个完整的球对应的立体角是 $4\pi$ 球面度

立体角（Solid Angle, $\mathrm{\Omega }$）

• 定义：描述空间中某个方向的角度范围。
• 公式：$$\mathrm{\Omega }=\int {\int }_{\text{区域}}\sin \theta \mathrm{d}\theta \mathrm{d}\varphi$$其中 $\theta$ 是极角，$\varphi$ 是方位角。
• 单位：球面度（sr, steradian）。
• 作用：用来描述方向性区域的大小。

Radiant Energy（辐射能量，$Q$）

• 定义：光的总能量，单位是焦耳（J）。
• 在光线追踪中的意义：描述光源发射的能量总量。
• 公式：辐射能量是所有后续量的基础。

辐射通量（Radiant Flux, $\mathrm{\Phi }$）

• 定义：光源每秒发出的能量总量。
• 公式：$$\mathrm{\Phi }\equiv \frac{\mathrm{d}Q}{\mathrm{d}t}$$
• 单位：瓦特（W）Or lm (Lumen)
• 作用：描述光的总功率，是衡量光的能量输出的基本量。

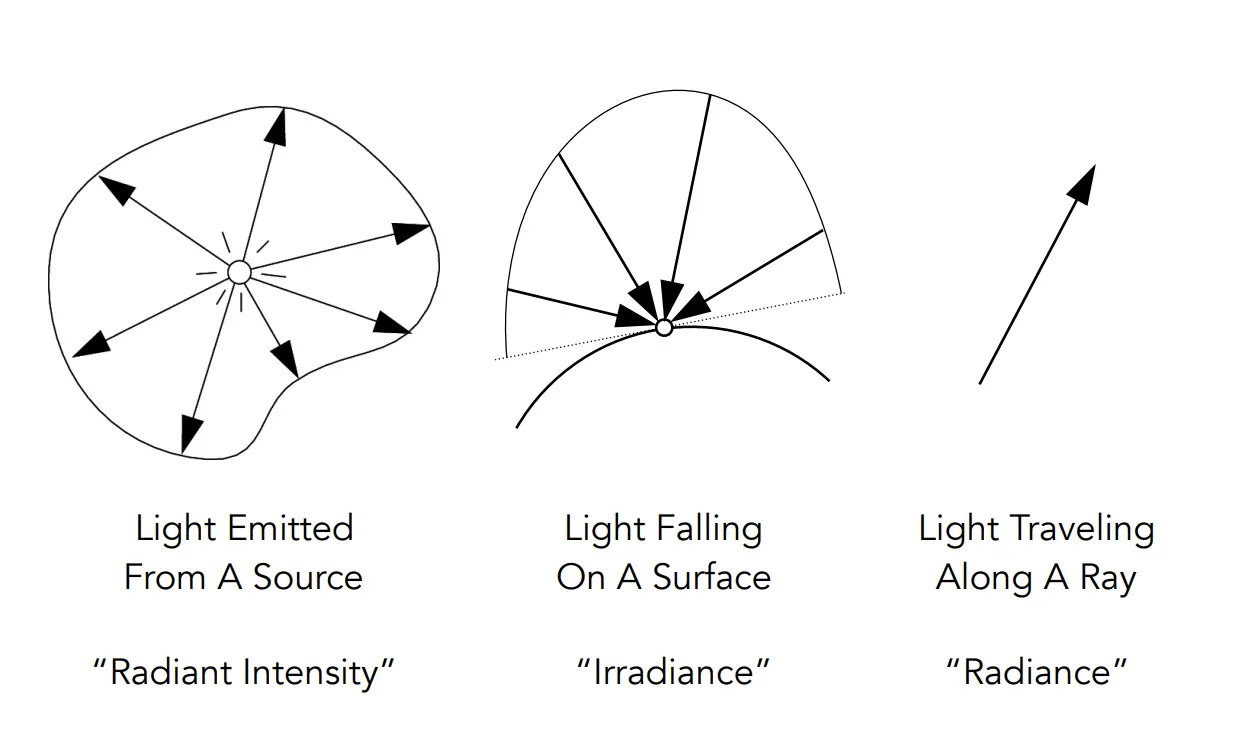
辐射强度（Radiant Intensity, $I$）

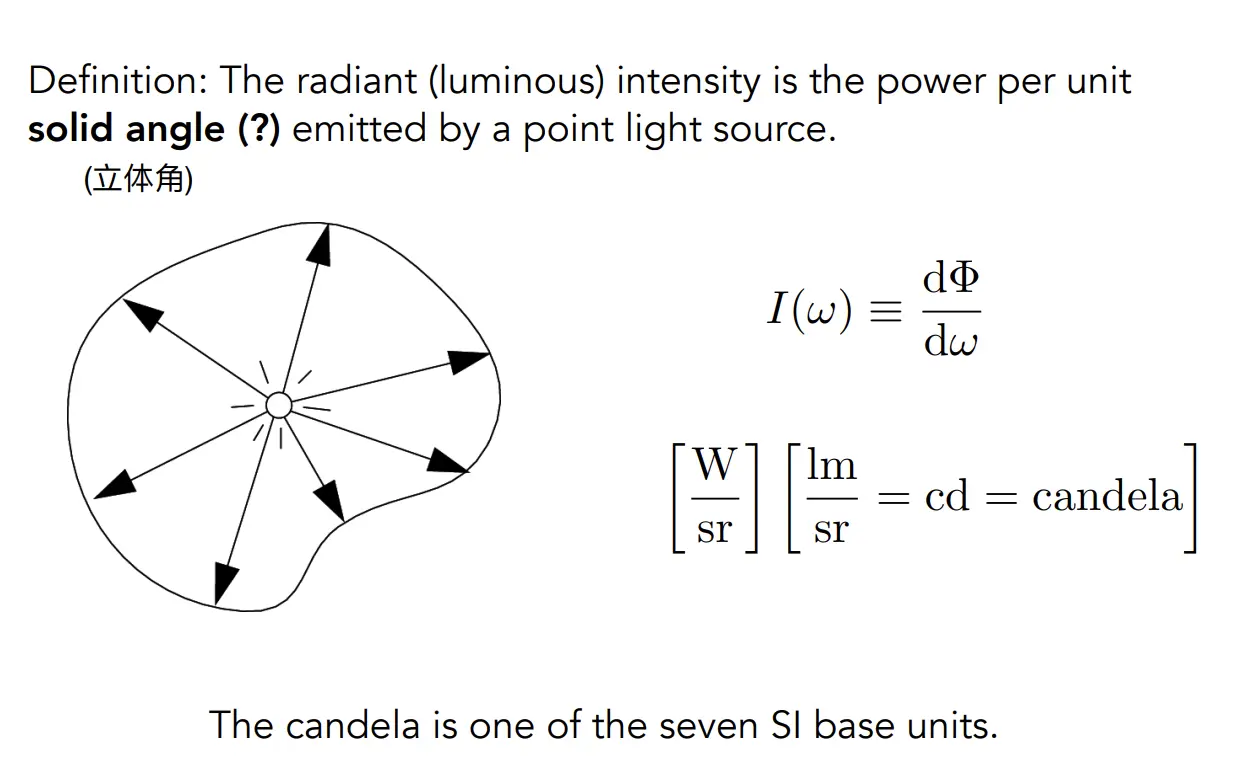
• 定义：在某个方向上的单位立体角中发出的辐射通量。
• 公式：$$I=\frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\mathrm{\Omega }}$$其中 $\mathrm{d}\mathrm{\Omega }$ 是立体角。
• 单位：瓦特每球面度（W/sr）。
• 作用：描述光源的方向性发光能力。

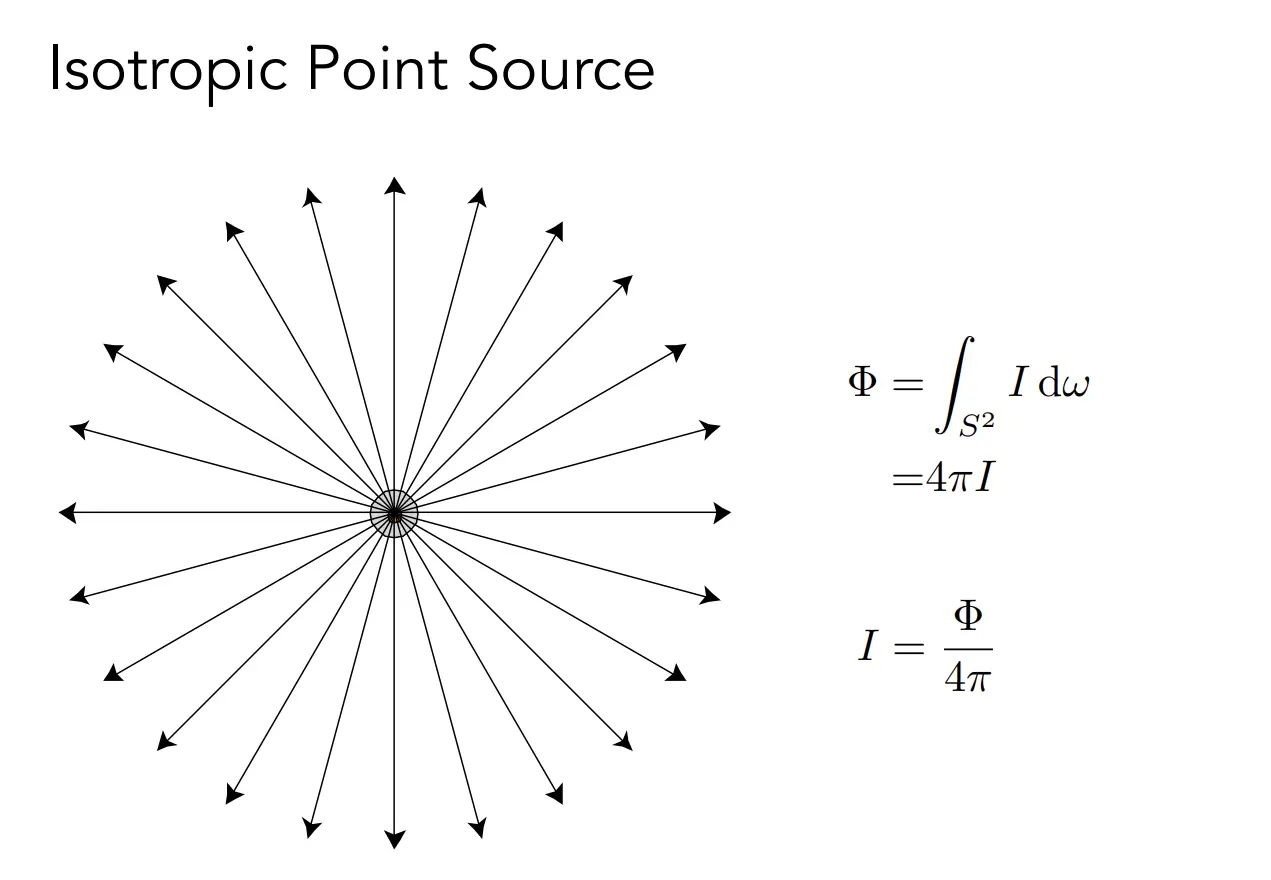
每秒辐射出来的总功率是$\mathrm{\Phi }$, 每个球面角上的辐射强度是$I$, 那么对全部球面角的辐射强度积分就是：

$$\mathrm{\Phi }=4\pi I$$

所以，辐射强度可以写成：

$$I=\frac{\mathrm{\Phi }}{4\pi }$$

辐射亮度（Radiance, $L$）

• 定义：描述单位面积和单位立体角内的辐射通量。
• 公式：$$L=\frac{{\mathrm{d}}^2\mathrm{\Phi }}{\mathrm{d}A\cos \theta \mathrm{d}\mathrm{\Omega }}$$其中：
  • $\mathrm{d}A$ 是表面面积；
  • $\theta$ 是与表面法线的夹角。
• 单位：瓦特每平方米每球面度（W/m²/sr）。
• 作用：是光线追踪的核心量，用于衡量光的方向和强度。

辐照度（Irradiance, $E$）

• 定义：单位面积上接收到的辐射通量。
• 公式：$$E=\frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}A}$$
• 单位：瓦特每平方米（W/m²）。
• 作用：衡量光照到物体表面的强度。