cross product

叉乘的两个应用：

• 判断左右
• 判断里外 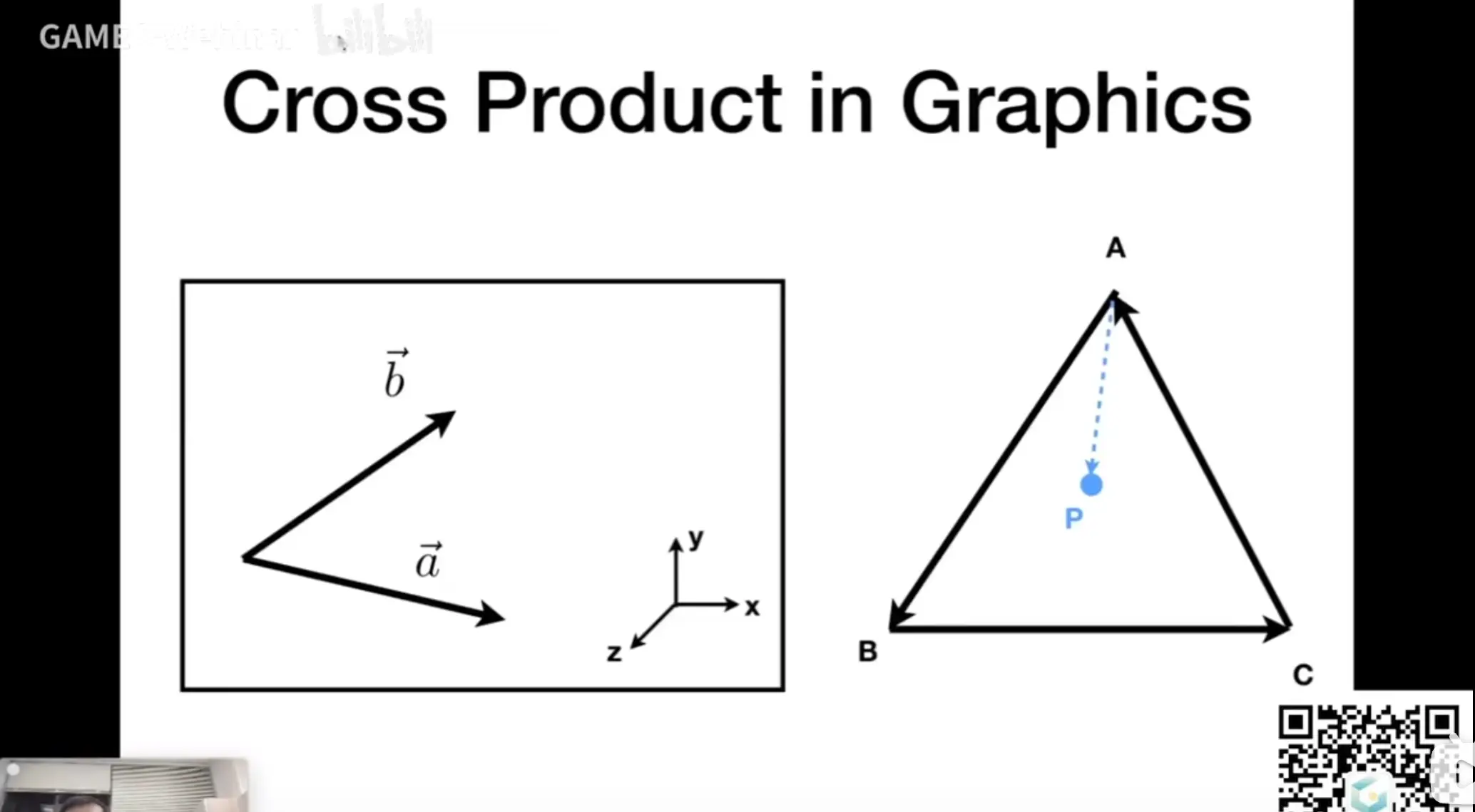比如光栅化就会用到，判断像素是否在三角形内部。如果是0，代表edge cases，自己决定。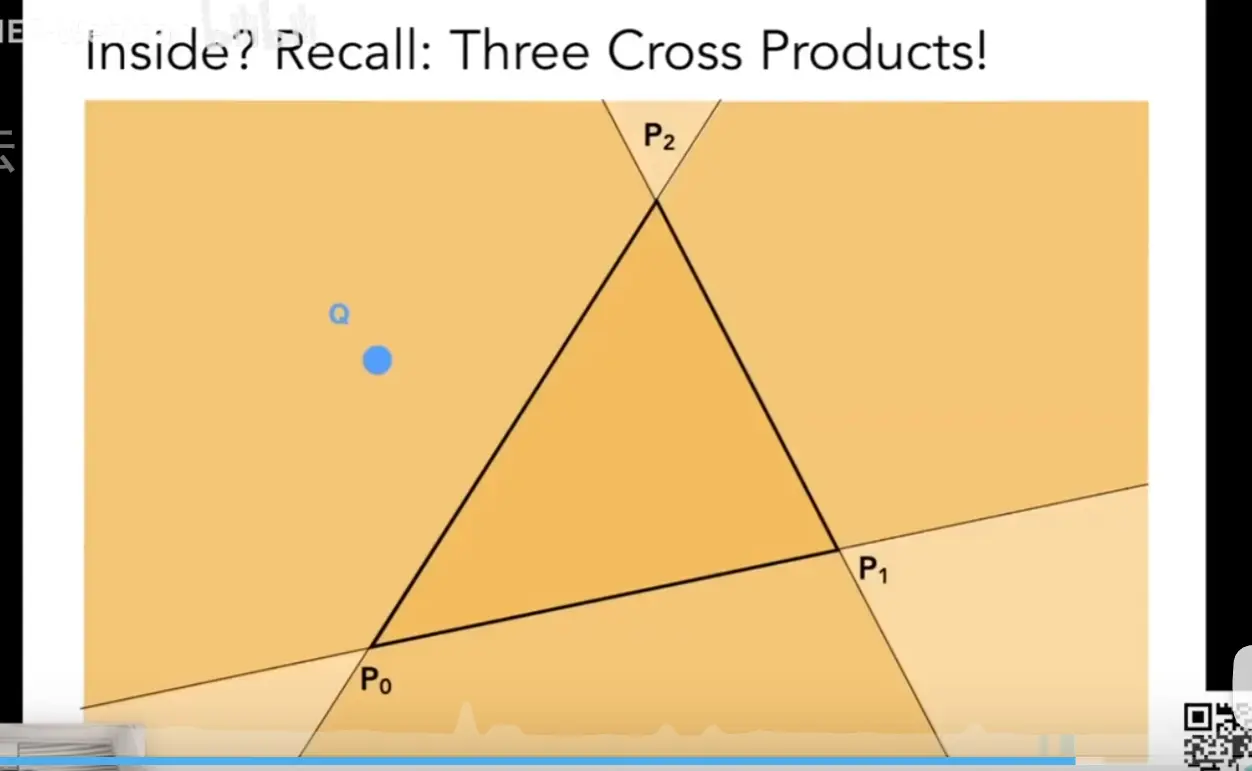

四元数乘法

四元数（Quaternion） 主要用于表示旋转，避免万向锁（Gimbal Lock）问题，同时提供更平滑的插值（如球面线性插值 Slerp）

在 Unreal Engine（UE5）中，四元数的乘法遵循 复合旋转（Composite Rotation） 的规则，即 右乘（Post-Multiplication） 规则：

NewRotation = RotationB * RotationA

• 先应用 RotationA，再应用 RotationB。

C++ 代码

#include "Math/Quat.h"

// 定义两个四元数
FQuat RotationA = FQuat(FRotator(0, 45, 0)); // 绕 Yaw 轴旋转 45 度
FQuat RotationB = FQuat(FRotator(0, 0, 30)); // 绕 Roll 轴旋转 30 度

// 计算合并旋转（先 Roll 30°，再 Yaw 45°）
FQuat ResultQuat = RotationB * RotationA;

// 转换为 Rotator（方便调试）
FRotator FinalRotator = ResultQuat.Rotator();
UE_LOG(LogTemp, Warning, TEXT("Final Rotation: %s"), *FinalRotator.ToString());

常用函数

FQuat 构造函数

//默认四元数
FQuat(float X, float Y, float Z, float W);
FQuat Q = FQuat();  // 等效于 FQuat(0, 0, 0, 1)

//以 单位轴向量 Axis 和 角度（弧度制） AngleRad 创建旋转
FQuat(const FVector& Axis, float AngleRad);
FQuat Q = FQuat(FVector(0, 0, 1), FMath::DegreesToRadians(90));  // 绕 Z 轴 90° 旋转

//从 欧拉角 FRotator 转换
FQuat(const FRotator& Rotator);
FRotator Rot = FRotator(0, 90, 0);  // 绕 Yaw 轴旋转 90°
FQuat Q = FQuat(Rot);  // 转换成四元数
FQuat Q = FRotator(0, 90, 0).Quaternion(); //等效

//从旋转矩阵 FMatrix 创建四元数
FQuat(const FMatrix& RotationMatrix);
FMatrix RotationMatrix = FRotationMatrix::MakeFromX(FVector(1, 0, 0));  // 让 X 轴朝向 (1, 0, 0)
FQuat Q = FQuat(RotationMatrix);

FQuat::FindBetweenNormals()

FQuat FindBetweenNormals(const FVector& Normal1, const FVector& Normal2); 输入参数也必须是单位向量，否则结果会出错。

这里的 Normal 指的是单位向量，和 FVector::GetSafeNormal() 一样。不是平面法向那个normal。

它结果N1到N2的最短旋转四元数，本质上是一个相对量。

所以想要应用这个“增量”的话，需要和当前的四元数相乘。

	template<typename T>
	TQuat<T> TQuat<T>::FindBetweenNormals(const TVector<T>& A, const TVector<T>& B)
	{
		const T NormAB = 1.f;
		return UE::Math::FindBetween_Helper(A, B, NormAB);
	}

	template<typename T>
	TQuat<T> TQuat<T>::FindBetweenVectors(const TVector<T>& A, const TVector<T>& B)
	{
		const T NormAB = FMath::Sqrt(A.SizeSquared() * B.SizeSquared());
		return UE::Math::FindBetween_Helper(A, B, NormAB);
	}

FindBetweenNormals() 只是 FindBetweenVectors() 的优化版本，它假设 A 和 B 已经是单位向量，从而省去 NormAB 计算

数学原理

数学原理

在 四元数中，四个分量 (X, Y, Z, W) 组成：

$$Q=(x,y,z,w)$$

其中：

• (X, Y, Z) 是旋转轴的方向，最快让物体到达目标角度的轴。
• W 由旋转角度计算得出，它决定了旋转的大小。

---

📌 四元数的旋转公式

如果想围绕 单位轴向量 Axis = (a, b, c) 旋转 θ（弧度），那么四元数的计算方式是：

$$Q=(X,Y,Z,W)=(a\cdot \sin (\theta /2),b\cdot \sin (\theta /2),c\cdot \sin (\theta /2),\cos (\theta /2))$$

其中：

• (a, b, c) 是旋转轴的单位向量。
• θ/2 是角度的一半。

---

📌看懂 (x, y, z, w)

FQuat Q(0.0f, 0.0f, 0.707f, 0.707f);

这里：

• X = 0.0f
• Y = 0.0f
• Z = 0.707f
• W = 0.707f

可以推导：

$$Z=\sin (\theta /2)=0.707$$$$W=\cos (\theta /2)=0.707$$

查表可知：

$$\theta /2=45°=\frac{\pi }{4}\text{（弧度）}$$

所以：

$$\theta =90°=\frac{\pi }{2}$$

即，Q 代表沿 Z 轴旋转 90°！

---

📌 计算绕任意轴旋转 90° 的四元数

假设 绕 Axis = (a, b, c) 旋转 90°（π/2 弧度），四元数计算如下：

float AngleRad = FMath::DegreesToRadians(90);  // 转换为弧度
FVector Axis = FVector(0, 0, 1).GetSafeNormal();  // 旋转轴（单位向量）

FQuat RotationQuat(Axis * FMath::Sin(AngleRad / 2), FMath::Cos(AngleRad / 2));

展开后：

$$X=0\times \sin (45°)=0.0$$$$Y=0\times \sin (45°)=0.0$$$$Z=1\times \sin (45°)=0.707$$$$W=\cos (45°)=0.707$$

得到：

FQuat(0.0f, 0.0f, 0.707f, 0.707f);

完全匹配 FQuat(0.0f, 0.0f, 0.707f, 0.707f)，所以它代表 绕 Z 轴 90° 旋转。

📌 其他旋转轴的示例

旋转轴	旋转角度	四元数
绕 X 轴 90°	(1, 0, 0)	FQuat(0.707f, 0.0f, 0.0f, 0.707f)
绕 Y 轴 90°	(0, 1, 0)	FQuat(0.0f, 0.707f, 0.0f, 0.707f)
绕 Z 轴 90°	(0, 0, 1)	FQuat(0.0f, 0.0f, 0.707f, 0.707f)

案例

物体围绕中心点旋转

void AMyActor::RotateAroundPoint(FVector Center, float DeltaTime)
{
    // 计算当前到中心的向量
    FVector ToCenter = GetActorLocation() - Center;

    // 计算旋转四元数（每秒旋转 45°）
    float RotationSpeed = 45.0f;
    FQuat RotationQuat = FQuat(FVector(0, 0, 1), FMath::DegreesToRadians(RotationSpeed * DeltaTime));

    // 计算新的位置
    FVector NewPosition = RotationQuat.RotateVector(ToCenter) + Center;

    // 应用位置
    SetActorLocation(NewPosition);

    // 让物体自身保持旋转
    AddActorWorldRotation(FRotator(0, RotationSpeed * DeltaTime, 0));
}

角色朝向目标（LookAt 方向旋转）

void AMyCharacter::RotateTowardsTarget(FVector TargetLocation, float DeltaTime)
{
    // 获取当前旋转（四元数）
    FQuat CurrentRotation = GetActorRotation().Quaternion();

    // 计算目标方向
    FVector Direction = (TargetLocation - GetActorLocation()).GetSafeNormal();
    FQuat TargetRotation = FQuat::FindBetweenNormals(GetActorForwardVector(), Direction);

    // 平滑插值（使用 DeltaTime 进行时间缩放）
    float RotationSpeed = 5.0f; // 旋转速度（越大旋转越快）
    float Alpha = FMath::Clamp(RotationSpeed * DeltaTime, 0.0f, 1.0f);
    FQuat NewRotation = FQuat::Slerp(CurrentRotation, TargetRotation * CurrentRotation, Alpha);

    // 应用旋转
    SetActorRotation(NewRotation);
}

Matrix

• 要能相乘，N要相同，然后结果 把N看出消掉了即可
• 计算结果，加入是第i行，第j列，那么就去A找第i行的全部元素，和B第J列的全部元素，点积即可。

点积 和 交积

• 点积 判断相似度，计算角度
• 叉积 判断左右，判断点是否在多边形内部 根据A x B = -B X A, 一旦有一条边符号不对，既说明在 点不在多边形内部。

齐次坐标

缩放和旋转都能用2x2矩阵乘法来变化，唯独平移。在2维上， 齐次坐标是为了解决 平移无法写成矩阵乘法的形式构建出来的3x3矩阵，同时让让功能多样化。

• 平移 $T(tx,ty)=\left(\begin{array}{ccc}1& 0& tx\\ 0& 1& ty\\ 0& 0& 1\end{array}\right)$

• 缩放 $S(sx,sy)=\left(\begin{array}{ccc}sx& 0& 0\\ 0& sy& 0\\ 0& 0& 1\end{array}\right)$

• 旋转 $R(\theta )=\left(\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right)$

• 沿$x$轴方向的剪切： $S{h}_x(s{h}_x)=\left(\begin{array}{ccc}1& s{h}_x& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$ 其中，$s{h}_x$是沿$x$轴方向的剪切因子。

• 沿$y$轴方向的剪切： $S{h}_y(s{h}_y)=\left(\begin{array}{ccc}1& 0& 0\\ s{h}_y& 1& 0\\ 0& 0& 1\end{array}\right)$

结合律

矩阵乘法不可以进行交换律，但有结合律

$M=T(tx,ty)\cdot R(\theta )$

计算这个乘积：

$M=\left(\begin{array}{ccc}1& 0& tx\\ 0& 1& ty\\ 0& 0& 1\end{array}\right)\cdot \left(\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right)$

进行矩阵乘法：

$M=\left(\begin{array}{ccc}1\cdot \cos \theta +0\cdot \sin \theta +tx\cdot 0& 1\cdot -\sin \theta +0\cdot \cos \theta +tx\cdot 0& 1\cdot 0+0\cdot 0+tx\cdot 1\\ 0\cdot \cos \theta +1\cdot \sin \theta +ty\cdot 0& 0\cdot -\sin \theta +1\cdot \cos \theta +ty\cdot 0& 0\cdot 0+1\cdot 0+ty\cdot 1\\ 0\cdot \cos \theta +0\cdot \sin \theta +1\cdot 0& 0\cdot -\sin \theta +0\cdot \cos \theta +1\cdot 0& 0\cdot 0+0\cdot 0+1\cdot 1\end{array}\right)$

简化结果：

$M=\left(\begin{array}{ccc}\cos \theta & -\sin \theta & tx\\ \sin \theta & \cos \theta & ty\\ 0& 0& 1\end{array}\right)$

因此，复合变换矩阵 $M$ 就是：

$M=\left(\begin{array}{ccc}\cos \theta & -\sin \theta & tx\\ \sin \theta & \cos \theta & ty\\ 0& 0& 1\end{array}\right)$

这个矩阵可以用于将二维点先旋转 $\theta$ 角度，然后平移 $(tx,ty)$。

蒙特卡洛积分（Monte Carlo Integration）

几何上，定积分表示的是曲线 $y=f(x)$ 与 $x$ 轴之间，从 $x=a$ 到 $x=b$ 的面积（有正负）。

计算函数 $y=x$ 在区间 $[0,1]$ 上的定积分：

$I={\int }_0^{1}xdx$ 即使忘了 积分的基本规则，也能回想起三角形的面积公式作为互补验证。找出它的原函数： $\int xdx=\frac{x^2}{2}+C$ 将 $x$ 从 $0$ 积分到 $1$：

$I={\left[\frac{x^2}{2}\right]}_0^1=\frac{1^2}{2}-\frac{0^2}{2}=\frac{1}{2}$ 定积分可以精准地算出积分值。而蒙特卡洛积分是离散的，算出的值也是大概值。下面请GPT来解释：

数学背景

蒙特卡洛积分的基本思想是通过随机采样来估计积分值。假设要计算一个函数 $f(x)$ 在区间 $[a,b]$ 上的积分：

$I={\int }_a^{b}f(x)dx$

蒙特卡洛方法通过在区间 $[a,b]$ 上随机采样 $N$ 个点 $x_i$，然后计算这些点上的函数值的平均值来近似积分：

$I\approx \frac{b-a}{N}\sum _{i=1}^{N}f(x_i)$

几何解释

虽然蒙特卡洛方法使用离散的采样点，但其几何解释仍然可以理解为曲线 $y=f(x)$ 与 $x$ 轴之间的面积。具体原因如下：

• 离散采样点的平均值：这些采样点的函数值平均值代表了函数在区间 $[a,b]$ 上的平均高度。
• 乘以区间长度：将平均高度乘以区间长度 $(b-a)$，得到的结果就是一个近似面积。

示例

假设要计算函数 $f(x)=x^2$ 在区间 $[0,1]$ 上的积分：

$I={\int }_0^1{x}^{2}dx$

使用蒙特卡洛方法：

1. 在区间 $[0,1]$ 上随机采样 $N$ 个点 $x_i$。
2. 计算这些点上的函数值 $f(x_i)=x_i^2$。
3. 计算这些函数值的平均值，并乘以区间长度 $(1-0)=1$。

公式为：

$I\approx \frac{1-0}{N}\sum _{i=1}^N{x}_i^2=\frac{1}{N}\sum _{i=1}^N{x}_i^2$

尽管是通过离散的采样点来进行计算，但最终结果仍然是对连续函数 $f(x)=x^2$ 在区间 $[0,1]$ 上积分的一个近似值，也就是曲线 $y=x^2$ 与 $x$ 轴之间的面积。

蒙特卡洛方法的优势

蒙特卡洛方法的优势在于它特别适用于高维积分和复杂函数的积分计算。在这些情况下，传统的数值积分方法（如梯形法、辛普森法）可能会由于维数灾难而变得不可行。而蒙特卡洛方法的计算复杂度与维数无关，只依赖于采样点的数量，因此在高维空间中表现尤为出色。

应用

蒙特卡洛积分在光线追踪（Ray Tracing）和全局光照（Global Illumination）中被广泛使用。通过模拟光线在场景中的传播和反射，可以生成高度逼真的图像。具体应用包括：

• 路径追踪（Path Tracing）：用于计算光线在场景中的多次反射和折射。
• 环境光遮蔽（Ambient Occlusion）：用于计算场景中各点的光照遮蔽程度。

在统计学和数据科学中，蒙特卡洛方法用于估计复杂概率分布的参数。例如：

• 贝叶斯推断：通过模拟后验分布来进行参数估计。
• 马尔可夫链蒙特卡罗（MCMC）：用于从复杂概率分布中采样。